Содержание
Математик-пенсионер, «хакнувший» лотерею / Хабр
Любитель головоломок
Джеральд Селби всегда любил загадки: там, где другие видели лишь шум, он стремился найти порядок и гармонию. Работая на фабрике Kellogg’s по производству овсяных хлопьев, он занимался анализом материалов для увеличения срока годности продукции. Однажды, изучая хлопья других компаний, Джерри наткнулся на странную последовательность символов на обороте коробки General Mills. Вместо даты и фабрики-производителя там был отпечатан загадочный код. Джерри решил расшифровать его: взяв несколько коробок завтраков Kellogg’s и General Mills, он начал сравнивать их влажность, сообразив, что хлопья с примерно одинаковой влажностью должны иметь близкие даты производства. Делая записи на бумаге, он выявил некоторые закономерности. Вскоре ему удалось расшифровать всё, что позволило определить место, дату и время изготовления. В более агрессивной сфере бизнеса «взлом» секретов конкурентов мог бы обернуться огромной выгодой, но не в производстве овсяных хлопьев, поэтому руководство восприняло его открытие без энтузиазма.
Однако Джерри это не расстроило — ему просто нравилось разбираться, как изнутри устроен мир и его отдельные части. В детстве он страдал дислексией, испытывая трудности с чтением домашних заданий, однако после стандартизированного теста в восьмом классе выяснил, что обладает навыками учёного. Выпустившись из старшей школы, он женился на своей однокласснице Марджори, сменил несколько работ и завёл шестерых детей, не переставая постоянно учиться. Он получил образование в общественном колледже Kellogg, степень бакалавра по математике и бизнесу, а также MBA в Университете Западного Мичигана. Всё это время он не давал передышки своему мозгу. Чтобы его увлечения не мешали семейной жизни, Джерри вовлёк в них детей. Когда его начинали интересовать грибы, он брал детей с собой в лес; влюбившись в геологию, он брал их искать в карьерах окаменелости. Наконец Джерри понял, что пора начинать работать на себя, и решил открыть небольшой магазин. Семья переехала в Эварт, штат Мичиган.
Магазин Corner Store, в котором Джерри впервые заинтересовался лотереей
Математически выверенный магазин
Эварт — 1903 жителя, три банка, один «Макдоналдс», единственный светофор на весь город. Селби выбрал этот город не просто так — несмотря на его провинциальность, он находился рядом с потоками автомобильного движения, а наличие поблизости заводов General Motors и Chrysler обеспечивало наличие покупателей. Через магазин регулярно проходили заводские рабочие, юристы и банкиры, которых Джерри знал если не по именам, то хотя бы по покупкам, которые они обычно совершали. В управлении своим бизнесом он тоже нашёл интересную математическую задачу и стремился максимально оптимизировать использование каждого метра площади. Например, он знал, что производители сигарет платят владельцам лавок определённой площади за размещение своей продукции, продавая им каждый блок со скидкой. Воспользовавшись этим, математик начал покупать сигареты оптом и продавать их тем магазинам, которым не давали скидок.
Селби выбрал этот город не просто так — несмотря на его провинциальность, он находился рядом с потоками автомобильного движения, а наличие поблизости заводов General Motors и Chrysler обеспечивало наличие покупателей. Через магазин регулярно проходили заводские рабочие, юристы и банкиры, которых Джерри знал если не по именам, то хотя бы по покупкам, которые они обычно совершали. В управлении своим бизнесом он тоже нашёл интересную математическую задачу и стремился максимально оптимизировать использование каждого метра площади. Например, он знал, что производители сигарет платят владельцам лавок определённой площади за размещение своей продукции, продавая им каждый блок со скидкой. Воспользовавшись этим, математик начал покупать сигареты оптом и продавать их тем магазинам, которым не давали скидок.
Год спустя после покупки Corner Store Джерри решил поставить в магазине автомат для лотереи — небольшой ящик, печатающий билеты лотереи штата Мичиган. Этот автомат был единственным в Эварте, он быстро приобрёл популярность и дело пошло. Вскоре магазин начал ежегодно продавать билетов на 300 тысяч долларов, из которых Селби оставалось 20 тысяч. Автомат оказался настолько успешным, что семейная пара смогла построить небольшую пристройку к магазину и наняла ещё одного работника для работы с лотереей. Благодаря доходам Селби смогли оплатить обучение всех шестерых детей, получивших учёные степени.
Вскоре магазин начал ежегодно продавать билетов на 300 тысяч долларов, из которых Селби оставалось 20 тысяч. Автомат оказался настолько успешным, что семейная пара смогла построить небольшую пристройку к магазину и наняла ещё одного работника для работы с лотереей. Благодаря доходам Селби смогли оплатить обучение всех шестерых детей, получивших учёные степени.
Шансы
И так продолжалось более пятнадцати лет. Наконец, в 2000 году Джерри и Мардж решили, что пора отправляться на пенсию. Джерри продал магазин и время от времени навещал новых хозяев, чтобы узнать, как идут дела. Однажды, в 2003 году он увидел в Corner Store брошюру с рекламой новой лотереи Winfall. Билет стоил 1 доллар. Игрок выбирал шесть чисел от 1 до 49. Если ему удавалось угадать все шесть чисел, то он получал джекпот от 2 миллионов долларов и более. Если угадать пять, четыре, три или два числа из шести, то игрока тоже ждал выигрыш. Однако заинтересовала Джерри любопытная особенность игры, так называемый «перелив»: если никто долгое время не выигрывал джекпот и он повышался до 5 миллионов, то происходил «перелив» этой суммы вниз, на победителей, угадавших меньшее количество чисел. «Перелив» происходил примерно через каждые шесть недель. В брошюре приводились шансы отгадывания комбинаций: Джерри увидел, что существует вероятность 1/54 подобрать три числа и выиграть 5 долларов, вероятность 1/1500 угадать четыре и выиграть 100 долларов. Проделав вычисления в уме, он понял, что игрок, дождавшийся «перелива», имел вероятность выиграть больше, чем потерять, если в розыгрыше «перелива» никто не угадывал все шесть чисел и не выигрывал джекпот. При этом джекпот распределялся на меньшие комбинации чисел, и три угаданных числа приносили выигравшему не 5, а 50 долларов, а четыре — не 100, а 1000. Внезапно вероятность начинала играть на стороне покупателей билетов! С точки зрения статистики, билет за 1 доллар в момент «перелива» имел бОльшую, чем номинал, ценность.
«Перелив» происходил примерно через каждые шесть недель. В брошюре приводились шансы отгадывания комбинаций: Джерри увидел, что существует вероятность 1/54 подобрать три числа и выиграть 5 долларов, вероятность 1/1500 угадать четыре и выиграть 100 долларов. Проделав вычисления в уме, он понял, что игрок, дождавшийся «перелива», имел вероятность выиграть больше, чем потерять, если в розыгрыше «перелива» никто не угадывал все шесть чисел и не выигрывал джекпот. При этом джекпот распределялся на меньшие комбинации чисел, и три угаданных числа приносили выигравшему не 5, а 50 долларов, а четыре — не 100, а 1000. Внезапно вероятность начинала играть на стороне покупателей билетов! С точки зрения статистики, билет за 1 доллар в момент «перелива» имел бОльшую, чем номинал, ценность.
В голове Джерри зародилась идея, но поначалу ему нужно было скрывать своё рискованное предприятие от Мардж — она всегда была прагматичной и не любила авантюры. Свои первые игры Джерри решил втайне моделировать на листе бумаги. Он выбрал числа на момент «перелива», дождался розыгрыша и подсчитал свой выигрыш. В теории ему удалось заработать.
Он выбрал числа на момент «перелива», дождался розыгрыша и подсчитал свой выигрыш. В теории ему удалось заработать.
Когда в следующий раз джекпот Winfall добрался до 5 миллионов и штат объявил о «переливе», Джерри отправился в магазин в 47 милях от Эварта, чтобы никто не задавал ему лишних вопросов. Подойдя к лотерейному автомату, он потратил 2200 долларов, позволив выбирать числа компьютеру. В день розыгрыша Джерри перебрал 2200 билетов и обвёл все совпадения из двух, трёх и четырёх чисел (совпадений из пяти чисел у него не было). В сумме его выигрыш составил 2150 долларов — чуть меньше, чем он потратил на билеты. Менее уверенный в своей системе человек мог на этом остановиться, но Джерри понял, что ему просто не повезло. Вероятности — это просто вероятности, а не гарантии. Его ошибка заключалась в том, что он рискнул слишком маленькой суммой. Во время следующего «перелива» Джерри снова вернулся в соседний город и купил билетов Winfall на 3400 долларов. На этот раз, чтобы его не уличила Мардж, он проверял выигрыши прямо в магазине, перебирая билеты вручную. В тот день ему удалось выиграть 6300 долларов. Набравшись смелости, он поставил на следующий «перелив» 8 тысяч и выиграл 15700 долларов.
В тот день ему удалось выиграть 6300 долларов. Набравшись смелости, он поставил на следующий «перелив» 8 тысяч и выиграл 15700 долларов.
Джерри решил поделиться своей тайной с женой, она дала согласие на дальнейшую игру. В конце концов, кого не убедят выигранные 15 тысяч?
Корпорация
Задача покупки крупных партий билетов оказалась непростой. Терминалы лотереи в магазинах могли печатать за раз только ленты по 10 билетов, то есть чтобы поставить на Winfall 100 тысяч долларов, нужно было ждать возле автомата, пока он напечатает 10 тысяч лент. Набираем код покупки. Нажимаем кнопку «Напечатать». Ждём не меньше минуты, пока появится 10 билетов. Вводим код следующей покупки. Нажимаем «Напечатать». Снова ждём. Джерри и Мардж знали всех владельцев продуктовых магазинов в городе, поэтому никто из них не мешал им, когда они приходили с утра и весь день печатали билеты. Семейство Селби связывало резинками для денег пачки билетов по 5 тысяч долларов, а потом в тишине своей гостиной собирало их в кучки в соответствии с выигрышем (ноль, два, три, четыре и пять совпавших номеров). Посчитав все билеты, они пересчитывали их снова, чтобы ничего не упустить. Постепенно они натренировались и на проверку каждого билета уходили считанные мгновения: взял, посмотрел, положил в стопку. Джерри и Мардж пытались привлечь к сортировке детей, но те за ними не поспевали, родители справлялись в десять раз быстрее.
Посчитав все билеты, они пересчитывали их снова, чтобы ничего не упустить. Постепенно они натренировались и на проверку каждого билета уходили считанные мгновения: взял, посмотрел, положил в стопку. Джерри и Мардж пытались привлечь к сортировке детей, но те за ними не поспевали, родители справлялись в десять раз быстрее.
Гараж, в котором Селби хранили все невыигравшие билеты на случай проверки налоговой
В июне 2003 года Джерри создал корпорацию для управления своей группой игроков, намеренно выбрав для неё скучное название GS Investment Strategies LLC. Он начал продавать в ней доли по 500 долларов, сначала своим детям, потом друзьям и коллегам из Эварта. Корпорация Джерри постепенно разрослась до 25 участников, в неё входили сотрудник полиции штата, инспектор по УДО, вице-президент банка, три юриста и даже его личный бухгалтер Стив Вуд.
Бизнес шёл хорошо: к весне 2005 года GS Investment Strategies LLC поучаствовала в 12 «переливах» Winfall, каждый раз увеличивая размеры ставок и выигрышей. Сначала прибыль составила 40 тысяч. Потом 80. Потом 160. Мардж перевела свою долю на свой депозит в банке. Джерри купил новый пикап и начал приобретать монеты Монетного двора США для защиты от инфляции, пытаясь оберегать свою семью на случай возможной катастрофы. Внезапно в мае 2005 года штат Мичиган без предупреждения прекратил проведение Winfall. Джерри это возмутило — у него отняли любимое дело, которое он создал благодаря своему математическому складу ума, дававшее ощущение цели в жизни.
Сначала прибыль составила 40 тысяч. Потом 80. Потом 160. Мардж перевела свою долю на свой депозит в банке. Джерри купил новый пикап и начал приобретать монеты Монетного двора США для защиты от инфляции, пытаясь оберегать свою семью на случай возможной катастрофы. Внезапно в мае 2005 года штат Мичиган без предупреждения прекратил проведение Winfall. Джерри это возмутило — у него отняли любимое дело, которое он создал благодаря своему математическому складу ума, дававшее ощущение цели в жизни.
На следующий месяц Джерри получил письмо от одного из членов его группы. Он заметил, что штат Массачусетс проводит похожую лотерею под названием Cash WinFall. Она слегка отличалась от мичиганской: билет стоил не один, а два доллара, числа выбирались от 1 до 46, а джекпот «переливался» вниз при превышении не пяти, а двух миллионов. Но в остальном она была практически такой же. Джерри прикинул вероятности на бумаге, они были хорошими. Поэтому он сел в свой пикап и совершил путешествие на 700 километров до города в Массачусетсе, где жил владелец магазина, который мог ему помочь. Джерри ещё не знал, что на этот раз столкнётся с безжалостными конкурентами.
Джерри ещё не знал, что на этот раз столкнётся с безжалостными конкурентами.
Столкновение
Семью месяцами ранее студент Массачусетского технологического института (MIT) Джеймс Харви предложил своим соседям по общежитию захватывающую авантюру. Джеймс учился на математика и для своего учебного исследовательского проекта изучал различия двух крупных лотерей, Powerball и MegaMillions, чтобы выяснить, в какой из них выше шансы выигрыша. Изучил он и местные лотереи штата, быстро обнаружив слабое место Cash WinFall. За считанные дни Харви привлёк к своей авантюре примерно пятьдесят человек, собрав с каждого по 20 долларов и купив 500 билетов лотереи. 7 февраля 2005 года команда из MIT выиграла 3 тысячи долларов, получив прибыль в 2 тысячи.
Любопытно, что студенты не были единственными, кто в то время играл в Cash WinFall на крупные суммы. Исследователь-биомедик из Бостонского университета Инь Чжан тоже обнаружил изъян лотереи. Учёный привлёк к игре своих друзей и организовал товарищество «Лотерейный клуб доктора Чжана». Его группа начала выигрывать в недели «перелива» по 300-500 тысяч долларов. Чжан уволился со своей работы, чтобы целиком погрузиться в лотерею.
Его группа начала выигрывать в недели «перелива» по 300-500 тысяч долларов. Чжан уволился со своей работы, чтобы целиком погрузиться в лотерею.
Однако возможности Чжана не могли сравниться с напором группы из MIT. После первого выигрыша сложилась группа из 40-50 игроков, многие из которых были профессорами со значительными финансовыми возможностями. В помощь по управлению группой Харви пригласил своего однокурсника Юйжаня Лу. Он помог Харви основать корпорацию Random Strategies LLC, которая стабильно покупала 300 тысяч билетов за 600 тысяч долларов. Студентам MIT было бы проще распечатывать билеты самостоятельно, а потом оплачивать их в магазинах, но по правилам массачусетской лотереи это было запрещено. Для защиты от мошенничества билеты обязательно нужно было покупать вручную.
Тем временем до Массачусетса добрался Джерри Селби. Он обратился к владельцу магазина Полу Мардасу с необычным предложением: для начала Джерри купит лотерейных билетов примерно на 100 тысяч. В обмен на это Мардас получает долю в GS Investment Strategies LLC. Пол согласился и спустя несколько дней Джерри вернулся с Мардж. Они решили разделить задачу печати билетов на двоих, поэтому стали искать второй магазин. Им стал Jerry’s Place в соседнем городе. Каждое утро Джерри с Мардж вставали в 5:30 и отправлялись печатать билеты, складывали их в пачки по 5 тысяч долларов.
Пол согласился и спустя несколько дней Джерри вернулся с Мардж. Они решили разделить задачу печати билетов на двоих, поэтому стали искать второй магазин. Им стал Jerry’s Place в соседнем городе. Каждое утро Джерри с Мардж вставали в 5:30 и отправлялись печатать билеты, складывали их в пачки по 5 тысяч долларов.
Billy’s Beverages Пола Мардаса в Сандерленде.
Jerry’s Place в Южном Дирфилде.
Суммы, регулярно уходящие на покупку билетов, постепенно дошли до 720 тысяч долларов — 360 тысяч билетов за один розыгрыш. Это никак не нарушало правила лотереи, поэтому Джерри чувствовал себя в безопасности. К тому же в 2008 году до него донеслись слухи, что в Cash WinFall участвует ещё одна большая группа, использующая похожие стратегии. Пять лет подряд Джерри с Мардж возвращались в Массачусетс по шесть-десять раз в год. Их система никогда не менялась: они печатали билеты, подсчитывали их в гостинице, получали один общий чек с выигрыша и возвращались обратно в Эварт с проигравшими билетами в багажнике. Однажды в магазин, где они покупали билеты, заглянул сотрудник лотереи, но не нашёл в действиях пары ничего незаконного.
Однажды в магазин, где они покупали билеты, заглянул сотрудник лотереи, но не нашёл в действиях пары ничего незаконного.
Подстава
Тем временем экономика США рушилась. Ипотечный кризис, спасение банков государством, банкротство автопроизводителей и паника, паника, паника. Завод Chrysler рядом с Эвартом закрылся, уволив более 120 человек.
У Селби же дела шли гораздо лучше. К 2009 году корпорация выиграла более 20 миллионов долларов (после вычетов налогов осталось 5 миллионов), однако образ жизни Джерри и Мардж не изменились. Они продолжали жить в том же доме и собирать невыигравшие билеты в гараже.
Однако группа из MIT в это время планировала атаковать игру с невиданным ранее уровнем агрессии. Хотя в конечном итоге её общий выигрыш за всё время составил 3,5 миллионов, прибыли падали из-за одной простой причины: конкуренции. Группа из MIT, Чжан и Селби должны была вливать для победы крупные суммы, а выигрыш им приходилось делить. Студенты решили найти способ выкинуть из игры остальные группы. Им пришла в голову идея: вместо того, чтобы дожидаться «перелива», можно устроить его самостоятельно, сделав огромную ставку. Перед розыгрышем WinFall 16 августа 2010 года штат не объявлял о «переливе», потому что джекпот не дотягивал до 1,6 миллиона и вероятность достижения 2 миллионов была мала. Харви с коллегами решили, что настало их время. За три дня они скупили целых 700 тысяч билетов, заплатив 1,4 миллиона долларов. Этого с запасом хватало, чтобы превзойти планку в 2 миллионов джекпота и вызвать «перелив». Об этом никто не знал, поэтому крупные игроки, в том числе Джерри с Мардж, не покупали билеты. В результате группа из MIT получила прибыль в 700 тысяч долларов.
Студенты решили найти способ выкинуть из игры остальные группы. Им пришла в голову идея: вместо того, чтобы дожидаться «перелива», можно устроить его самостоятельно, сделав огромную ставку. Перед розыгрышем WinFall 16 августа 2010 года штат не объявлял о «переливе», потому что джекпот не дотягивал до 1,6 миллиона и вероятность достижения 2 миллионов была мала. Харви с коллегами решили, что настало их время. За три дня они скупили целых 700 тысяч билетов, заплатив 1,4 миллиона долларов. Этого с запасом хватало, чтобы превзойти планку в 2 миллионов джекпота и вызвать «перелив». Об этом никто не знал, поэтому крупные игроки, в том числе Джерри с Мардж, не покупали билеты. В результате группа из MIT получила прибыль в 700 тысяч долларов.
Джерри был в ярости. Одно дело — совершать крупные ставки по определённой системе, как это делал он, и совершенно другое — манипулировать механикой игры, чтобы вытеснить конкурентов. «Они намеренно вывели нас из игры». Он решил, что когда в следующий раз группа из MIT попытается атаковать, он будет готов.
Он подозревал, что что-то произойдёт примерно на Рождество. Розыгрыш был назначен на 27 декабря, когда большинство магазинов будет закрыто. Из-за малой активности покупателей билетов это будет идеальное время для атаки MIT. Джерри попросил Мардаса связаться с организаторами лотереи и узнать, были ли пиковые продажи. Оказалось, что в пяти магазинах продажи резко увеличились. Оставив Мардж дома, Джерри отправился в Jerry’s Place, где потратил остаток дня на печать 45 тысяч билетов.
Уже допечатывая билеты в одиночестве, он услышал стук в дверь магазина. Вежливый молодой человек сказал, что его зовут Юран Лу. «Я из другого клуба, и думаю, было бы взаимовыгодно, если бы мы знали, сколько вкладывает в игру каждая из сторон». Ребята из MIT предложили договориться — вместо того, чтобы делать ставки всем вместе, логичнее играть по очереди. С точки зрения Джерри, это было неэтично, поэтому он отказался и закрыл дверь.
Конец игры
Получив информацию о загадочных выигрышах в массачусетской лотерее, журналист-расследователь из Boston Globe Андреа Эстес начала искать факты. Она изучила список самых больших счастливчиков и выяснила, что мичиганская компания GS Investment Strategies LLC массово скупала билеты в магазине Пола Мардаса. Запросив официальные данные, она обнаружила, что крупные покупки совершали как минимум ещё две группы. Эта информация стала фундаментом для статьи Андреа с заголовком «Игра с выигрышем для немногих знающих». В статье упоминались Джерри и Мардж, а также Лу. «Некоторые умники узнали, как становиться богатыми, пока остальные оплачивают их выигрыши». История вызвала сенсацию. Политики штата публично раскритиковали организацию лотереи, а сюжет подхватили СМИ национального уровня, такие как Washington Post, HuffPost и Fox News. Два дня спустя министр финансов штата Гроссман заявил, что розыгрыши Cash WinFall будут прекращены в течение года; тем временем, лотерея ограничит каждый магазин покупкой билетов на сумму не более 5 тысяч долларов в день.
Она изучила список самых больших счастливчиков и выяснила, что мичиганская компания GS Investment Strategies LLC массово скупала билеты в магазине Пола Мардаса. Запросив официальные данные, она обнаружила, что крупные покупки совершали как минимум ещё две группы. Эта информация стала фундаментом для статьи Андреа с заголовком «Игра с выигрышем для немногих знающих». В статье упоминались Джерри и Мардж, а также Лу. «Некоторые умники узнали, как становиться богатыми, пока остальные оплачивают их выигрыши». История вызвала сенсацию. Политики штата публично раскритиковали организацию лотереи, а сюжет подхватили СМИ национального уровня, такие как Washington Post, HuffPost и Fox News. Два дня спустя министр финансов штата Гроссман заявил, что розыгрыши Cash WinFall будут прекращены в течение года; тем временем, лотерея ограничит каждый магазин покупкой билетов на сумму не более 5 тысяч долларов в день.
Джерри не мог поверить — в статье его и других представили мошенниками, крупными игроками, наживающимися на обычных людях. Каким образом массовая скупка билетов оказалась жульничеством? Если уж обвинять кого-то в мошенничестве, так это саму лотерею, бравшую себе 40% от каждого купленного им билета. Он решил связаться с Эстес и наконец дать ей интервью, рассказав о настоящих манипуляциях с игрой — о том, как группа из MIT в 2010 году намеренно вызвала «перелив». Вышли ещё две статьи в Globe, ещё сильнее возмутив общественность, поэтому в октябре 2011 года Гроссман объявил, что попросил провести расследование процедур проведения лотереи.
Каким образом массовая скупка билетов оказалась жульничеством? Если уж обвинять кого-то в мошенничестве, так это саму лотерею, бравшую себе 40% от каждого купленного им билета. Он решил связаться с Эстес и наконец дать ей интервью, рассказав о настоящих манипуляциях с игрой — о том, как группа из MIT в 2010 году намеренно вызвала «перелив». Вышли ещё две статьи в Globe, ещё сильнее возмутив общественность, поэтому в октябре 2011 года Гроссман объявил, что попросил провести расследование процедур проведения лотереи.
В последний раз Джерри и Мардж играли в Cash WinFall в январе 2012 года. Это было невероятное приключение: в общей сумме за девять лет игры в двух штатах они заработали примерно 27 миллионов долларов. Прибыль составила 7,75 миллионов без вычета налогов, эти деньги были распределены среди игроков GS Investment Strategies LLC.
В свои 79 лет Джерри по-прежнему иногда играет в лотерею — в джекпот Powerball. (Он работает над системой выбора «выигрышных» номеров, но пока безуспешно. ) Время от времени он заходит в казино и играет в Texas Hold ’em. Мардж ходит с ним, но ей не нравятся азартные игры. Однажды Джерри дал ей 100 долларов для игры в «однорукого бандита», и в конце вечера Мардж вернула ему ту же сотню. Харви и Лу основали Интернет-стартап и занялись технологиями. Селби использовали свои выигрыши для развития нового бизнеса: финансирования строительства. Джерри даёт ссуды компаниям, строящим жильё, в том числе, и для бывших военных. «Мардж — один из самых крупных моих инвесторов», — говорит он.
) Время от времени он заходит в казино и играет в Texas Hold ’em. Мардж ходит с ним, но ей не нравятся азартные игры. Однажды Джерри дал ей 100 долларов для игры в «однорукого бандита», и в конце вечера Мардж вернула ему ту же сотню. Харви и Лу основали Интернет-стартап и занялись технологиями. Селби использовали свои выигрыши для развития нового бизнеса: финансирования строительства. Джерри даёт ссуды компаниям, строящим жильё, в том числе, и для бывших военных. «Мардж — один из самых крупных моих инвесторов», — говорит он.
Спустя все эти годы Селби по-прежнему собираются с участниками лотерейной группы, вспоминая свои авантюры.
При написании статьи использовался следующий материал: highline.huffingtonpost.com/articles/en/lotto-winners
На правах рекламы
Какими бы не были ваши увлечения, всегда не помешают доступные и надёжные серверы.
Приобретая наши VDS вы получаете и то, и другое!
Математические формулы в лотерее, вероятности и комбинации
Математические формулы в лотерее являются частью теории вероятностей и комбинаторной математики.
Что же мы подразумеваем под этим интуитивным понятием вероятности? С точки зрения математики возможны две различные интерпретации этого сугубо абстрактного понятия. В первой из них понятие вероятности ассоциируется с частотой появления данного события в серии опытов, в каждом из которых анализируемое событие может появиться или не появиться. Такое событие математики называют случайным.
Существует так называемый закон больших чисел, справедливость которого доказывается в теории вероятностей. Согласно этому закону, в любой серии опытов при увеличении их числа, частота появления случайного события всегда стабильно стремится к одной и той же величине и это предельное значение можно принять за вероятность Р(А) (probability — на английском языке):
Таким образом, согласно этому утверждению, чтобы найти вероятность события, нужно провести достаточно длинную серию опытов и полученную частоту выразить в процентах.
А нельзя ли определить вероятность выигрыша априори, то есть до начала опытов? Оказывается, что в ряде случаев это возможно. Метод, который используется для априорного определения величин вероятности, основан на втором возможном варианте ее интерпретации и состоит он в следующем:
Метод, который используется для априорного определения величин вероятности, основан на втором возможном варианте ее интерпретации и состоит он в следующем:
то — есть вероятность появления события А равна отношению числа m — благоприятных событий для А к полному числу n — возможных элементарных событий, выраженному в процентах.
Рассмотрим теперь задачу, более близкую к нашим интересам. А эти интересы в данном случае связаны с подсчетом вероятностей угадывания цифр в розыгрышах Лото 6/49. По правилам этой игры, требуется угадать шесть отобранных (счастливых) номеров из общего количества имеющихся в наличии сорока девяти. Для наглядности заштрихуем «счастливые номера», как это показано на рисунке.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |
Какова вероятность того, что перевернутый номер окажется заштрихованным? Очевидно, она и в этом случае равна отношению числа благоприятных для нас исходов (заштрихованных номеров, а их число равно 6) к полному числу всех возможных исходов (то есть полному числу номеров, число которых 49). Таким образом, вероятность угадать одну из шести отобранных номеров равна 6/49, а вероятность не угадать, соответственно — 43/49.
Таким образом, вероятность угадать одну из шести отобранных номеров равна 6/49, а вероятность не угадать, соответственно — 43/49.
Если сложить теперь вероятности этих двух возможных исходов, то, как и следовало ожидать, сумма всех вероятностей окажется равной 1. Конечно, хоть что-нибудь, но должно же случиться с достоверностью (то есть с вероятностью 100%). Как говорят, уж если не выиграю, то проиграю.
При второй попытки полное число оставшихся номеров, уже становится равным 48 (один номер уже был разыгран в первом туре). Таким образом, для всех возможных вариантов исхода получаем:
- Если в первом туре был угадан заштрихованный номер:
Вероятность угадать заштрихованный номер становится равно 5/48, а вероятность выпадения незаштрихованного номера составит 43/48. - Если в первом туре был угадан незаштрихованный номер:
Вероятность угадать заштрихованный номер становится равно 6/48, а вероятность выпадения незаштрихованного номера составит 42/48.
Таким образом, при двух подходах жеребьевки возможны четыре варианта результата (первый подход + второй подход):
1) угадал + не угадал: p = 6/49 x 43/48 = 0,1097
2) не угадал + угадал: p = 43/49 x 6/48 = 0,1097
3) угадал + угадал: p = 6/49 x 5/48 = 0,0128
4) не угадал + не угадал: p = 43/49 x 42/48 = 0,7679
Нетрудно убедиться, что и в этом случае сумма вероятностей равна 1.
Легко заметить, что по мере увеличения количества подходов общее количество возможных вариантов результата увеличивается очень быстро, а именно: общее количество возможных вариантов результата для n подходов розыгрышей равно 2n (2 в степени n).
Например, при трех подходах у нас уже будет 23 = 8 возможных вариантов результата:
1) угадал + угадал + угадал: вероятность = 0,0011
2) угадал + угадал + не угадал: вероятность = 0,0117
3) угадал + не угадал + угадал: вероятность = 0,0117
4) не угадал + угадал + угадал: вероятность = 0,0117
5) угадал + не угадал + не угадал: вероятность = 0,0980
6) не угадал + угадал + не угадал: вероятность = 0,0980
7) не угадал + не угадал + угадал: вероятность = 0,0980
8) не угадал + не угадал + не угадал: вероятность = 0,6698
Зная общее количество возможных вариантов, давайте теперь выясним, сколько из этих вариантов содержат угаданные числа. Количество этих вариантов на самом деле является количеством всех возможных комбинаций угаданных заштрихованных чисел.
Количество этих вариантов на самом деле является количеством всех возможных комбинаций угаданных заштрихованных чисел.
Предположим, что мы отметили шесть произвольных чисел и хотим узнать, сколько существует вариантов, в которых будет угадано 4 цифры из 6. Число способов, которыми можно угадать 4 из этих 6 номеров, математики называют числом сочетаний и обозначают его . Эта запись читается так: «число сочетаний из шести по четыре».
Предположим, что угаданы числа 12, 14, 30 и 36. Сколько вариантов существует для такого угадывания? Число 12 может быть угадано в любой из 6 попыток, то-есть может быть названо 1-м, 2-м, 3-м, 4-м, 5-м или 6-м. Следовательно, для угадывания числа 12 существует 6 различных вариантов. Второе число 14 может быть угадано в любой из оставшихся пяти попытках, следовательно, для его угадывания имеется 5 различных вариантов. Продолжая эти рассуждения, легко прийти к выводу, что для угадывания числа 30 существует 4 различных варианта, а числа 36 — 3 варианта. Следовательно, для угадывания четверки чисел из шести «счастливых» существуют всего 6х5х4х3 вариантов.
Следовательно, для угадывания четверки чисел из шести «счастливых» существуют всего 6х5х4х3 вариантов.
Но не все эти варианты различны. Предположим, что эти числа были угаданы в первых же четырех попытках. Тогда все эти варианты, соответствующие различной последовательности заполнения «счастливых» номеров в тех же самых попытках (всего 24 варианта), фактически представляют 1 вариант (число перестановок 4 элементов равно 4х3х2х1=24).
Окончательно для искомого числа сочетаний мы получили формулу:
Эта формула для числа сочетаний является справедливой и при любых других количествах отмеченных чисел и количествах «угаданных». В общем случае можно сформулировать следующее правило: для того, чтобы определить количество возможных вариантов с m угаданными числами для отмеченных n чисел, необходимо вычислить число сочетаний:
В этой формуле число сомножителей в числителе и знаменателе одинаково и равно m.
Также по этой формуле рассчитывается общее количество возможных комбинаций для игр в лотереи. А для Лото 6 из 49 получаем:
А для Лото 6 из 49 получаем:
На основе формулы (*) заполняется таблица с количеством выигрышей для каждой категории выигрышей, в зависимости от того, сколько чисел было отмечено и сколько чисел было угадано. См. В качестве примера таблицу для Лото 6/49.
Теперь перейдем к оценке выигрышей, которые рассчитываются на основе среднего выигрыша одного игрового варианта, разыгранного для каждой призовой категории. Средний выигрыш представляет собой вероятность возникновения этого выигрыша, умноженную на общую сумму денег, предложенную для данной призовой категории.
Согласно математическим расчетам, средние значения выигрыша для каждого рубля, потраченного в простой игровой системе и в развернутой игровой системе, одинаковы, независимо от того, сколько чисел было отмечено. Но все же различие между этими двумя игровыми системами существует.
Если мы возьмем статистическую характеристику для большого количества участников игры, то заметим, что при увеличении количества отмеченных чисел в билете в целом, выигрыши становятся крупнее, но вероятность более мелких выигрышей при этом резко уменьшается.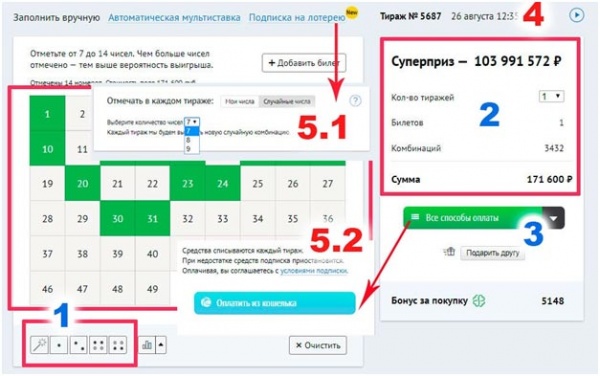 Отсюда можно сделать вывод, что если вы стремитесь только к крупному выигрышу, то для вас предпочтительнее будет развернутая система игры, но если не любите сильно рисковать и считаете, что лучше иметь «синицу в руках, чем журавля в небе», то лучше подойдет простая система игры.
Отсюда можно сделать вывод, что если вы стремитесь только к крупному выигрышу, то для вас предпочтительнее будет развернутая система игры, но если не любите сильно рисковать и считаете, что лучше иметь «синицу в руках, чем журавля в небе», то лучше подойдет простая система игры.
Какова вероятность длинной серии неудач, если ставить в каждом туре на одну и ту же комбинацию? Существует формула, которая называется формулой Бернулли. Она позволяет найти вероятность того, что в результате участия в n турах игры количество туров без единого выигрыша будет равно m:
где q определяет вероятность «несчастного» случая только для одного тура т.е. не были угаданы 6, 5 и 4 номеров и определяется формулой:
где , и вероятности угадывания 4-х, 5-ти и 6-ти чисел соответственно.
Для примера, на основе формулы Бернулли и некоторых исходных статистических данных были получены следующие результаты вероятностей неудач для 4 розыгрышей:
1) Не было ни одного выигрыша: m = 4, P = 0,02 (2%)
2) Был один выигрыш: m = 3, P = 0,13 (13%)
3) Было два выигрыша: m = 2, P = 0,33 (33%)
4) Было три выигрыша: m = 1, P = 0,37 (37%)
5) Все туры были выигрышными: m = 0, P = 0,15 (15%)
2% + 13% + 33% + 37% + 15% = 100%
Как видим, вероятность последовательных проигрышей с одной и той же комбинацией чисел уменьшается с увеличением количества участий, но появление выигрыша не гарантирует того, что он будет большим.
И все-таки, несмотря на то, что непредсказуемость результатов азартной игры является ее основной чертой, нельзя ли избрать какую-то оптимальную стратегию? Единственный совет, который можно дать в этом случае — это рационально выбрать определенную систему игры и последовательно придерживаться её.
Гарантированная система
для выигрыша в лотерею 6/49 Пошаговые инструкции — здесь!!
Автор: stacey,
в размышлениях о жизни
Я разработал систему, в которой каждый может выиграть в лотерею 6/49 или BC 49 каждую неделю, неделю за неделей. И система настолько проста, что я с удовольствием поделюсь ею с вами.
Я считаю, что ту же концепцию или систему можно использовать с Lotto Max, Lotto 6/49 или BC 49, хотя я еще не пробовал ее с Lotto Max.
Итак, позвольте мне объяснить, как я выигрываю лотерею 6/49 и BC 49 каждую неделю. Перед игрой на любые номера вам действительно следует открыть отдельный банковский счет, чтобы вносить свой выигрыш каждую неделю. Приятно иметь отдельный счет, где вы можете наблюдать за тем, как ваши выигрыши растут каждую неделю.
Приятно иметь отдельный счет, где вы можете наблюдать за тем, как ваши выигрыши растут каждую неделю.
Хотя вы можете играть в Lotto 6/49 и BC 49 два раза в неделю, я предпочитаю играть только раз в неделю. Я стараюсь не быть жадным.
Далее, как вам и всем разрешено, выберите шесть чисел. Сделайте их числами, которые значимы и запоминаются для вас непосредственно. Например, номер месяца (или года в некоторых случаях), когда вы в последний раз занимались сексом с вашим партнером, даты рождения, годовщины и т. д. Шесть чисел, которые вы не забудете. Запишите их и запомните.
Теперь отправляйтесь к местному продавцу лотереи Lotto 6/49 и возьмите одну из тех форм, которые вы используете для заполнения крошечных розовых прямоугольников, чтобы указать, какие номера вы выбираете. Обычно я играю комбо — 6/49 и BC 49 с Extra. Заполните форму своими номерами. Повторяйте числа снова и снова в уме, пока вы это делаете. Вам нужно вбить эти числа в свой разум, чтобы, когда вы едете или сидите на дерьме, они (цифры) повторялись почти бессознательно.
Теперь самое главное. со своей 5-долларовой купюрой и крепко сжатым в руке листком бумаги с маленькими карандашными розовыми прямоугольниками выходите из магазина своего розничного продавца Lotto 6/49. Быстро и не оглядываясь, подойдите к ближайшему банкомату и положите эту симпатичную синюю купюру на свой только что открытый банковский счет. Я рекомендую вам попробовать иметь купюру в 5 долларов, поскольку большинство банковских автоматов не одобряют, когда вы вносите монеты в автоматы. Они написали мне довольно неприятное письмо, когда я в последний раз пытался внести в автомат десять десятицентовиков, четыре четвертака, два луни и туни. Вся эта чепуха о том, что «вас могут привлечь к ответственности за расходы на ремонт и прочее бла-бла-бла». Банкиры…
На данный момент вы в плюсе на пять баксов. Довольно круто, а? Однако не думайте, что это конец волнения моей надежной системы. Становится лучше. И НАМНОГО интереснее. Подумайте о моменте, когда вы находитесь на вершине первого холма на американских горках-монстрах… это так захватывающе!!
Допустим, вы планировали сыграть в субботу вечером. Вы можете либо посмотреть цифры в субботу, либо просмотреть их в Интернете, в газете или в любой другой форме в воскресенье утром. Я стараюсь сидеть и пить расслабляющий кофе, когда проверяю, выпали ли мои номера.
Вы можете либо посмотреть цифры в субботу, либо просмотреть их в Интернете, в газете или в любой другой форме в воскресенье утром. Я стараюсь сидеть и пить расслабляющий кофе, когда проверяю, выпали ли мои номера.
И вот тут становится по-настоящему интересно… если ваши номера не выпали, как это было со мной за одну неделю до полного календарного года, тогда ВЫ ПРОСТО ВЫИГРАЛИ В ЛОТО!!! Ваши пять долларов лежат в банке и растут вместе с начисленными процентами, обычно по ставке 0,01% или по такой же прибыльной ставке.
Однако, если ваши номера нарисованы, те числа, которые крутятся в вашей голове день и ночь, ну извините, вы просто проиграли. Если большой приз, шесть из шести номеров совпадают с вашими… что ж, это действительно отстойно быть вами. Вы только что проиграли. И потерять… дерьмо, вы можете потерять 2,5 миллиона долларов, 4 миллиона долларов, 5 миллионов долларов или даже 10 миллионов долларов или больше. Вы можете не играть, когда у них есть этот месяц бонусных розыгрышей. Возбуждение может быть слишком сильным для некоторых людей. Парень, в первые несколько раз, когда ты играешь с моей системой, у тебя кажется, что желудок вот-вот выскочит из горла, ты так возбуждаешься!!
Возбуждение может быть слишком сильным для некоторых людей. Парень, в первые несколько раз, когда ты играешь с моей системой, у тебя кажется, что желудок вот-вот выскочит из горла, ты так возбуждаешься!!
Хорошей новостью является то, что в эти выходные я буду выигрывать в Лото 6/49 52 недели подряд! Теперь у меня есть 255 долларов на моем выигрышном счете в лотерею, и если я снова выиграю в эту субботу… сделаю это крутыми 260 долларами. О азарт!! Не могу дождаться этой субботы, когда смогу проверить, выиграл ли я снова лотерею 6/49!! Можешь представить!!
Нравится:
Нравится Загрузка…
Статистика алгоритма предсказания для лотереи Турция Лото 6-49.
фейсбук
- Блог
- Новости
- Связаться с нами
- Войти
- Регистр
- Войти
- Регистр
Выберите розыгрыш:
выбирать
вернуться в Турцию Лото 6-49
Лучшее предсказание алгоритма
Лото 6-49
Сб 18 июля 2015
выигрыш
TL45
Посмотреть прогноз
Предсказание последнего розыгрыша
Лото 6-49
Сб 02 января 2021
нет выигрыша
Посмотреть прогноз
Следующий розыгрыш
Сб 09 января 2021
Получить прогнозы алгоритма для выигрыша в лотерею
Получить прогнозы
Предыдущий алгоритм предсказывает успех
Сводка прогнозов
| Сводка | |
|---|---|
| Всего сделано прогнозов | 652 прогноза |
| Успешные предсказания | 60 прогнозов |
| Возможный выигрыш | 550 долларов США |
Последние выигрышные прогнозы
| Лотерея | Дата розыгрыша | Победа |
|---|---|---|
| Лото 6-49 | Сб 24 окт 2020 | (3 из 6) $5.  0 0✔ ВЫИГРЫШ
|
| Лото 6-49 | Сб, 20 июня 2020 г. | (4 из 6) $5.0 ✔ ВЫИГРЫШ
|
| Лото 6-49 | Сб 14 мар 2020 | (4 из 6) $5.  0 0✔ ВЫИГРЫШ
|
| Лото 6-49 | Сб 29февраль 2020 г. | (5 из 6) $40.0 ✔ ВЫИГРЫШ
|
| Лото 6-49 | Сб 29 фев 2020 | (3 из 6) $5. 
|
