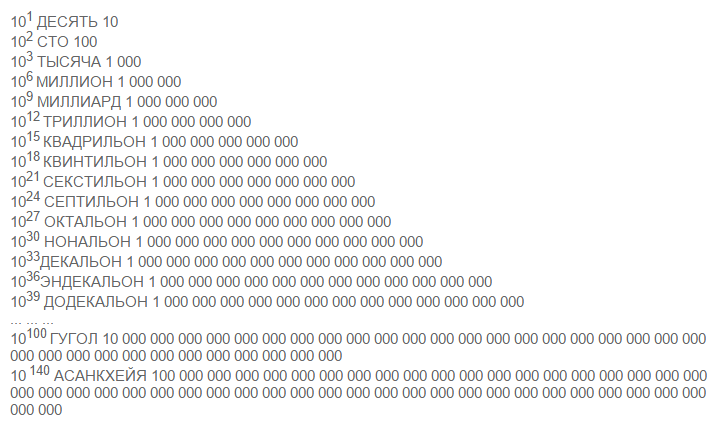|
|
|
|
|
|
|
|
|
|
Занимательная статистика. Часть вторая, гигантская. От миллиона 1
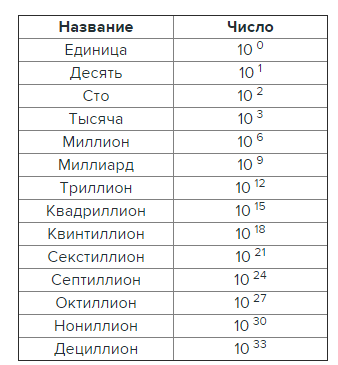
ochisle.ru Названия больших чисел | Формулы и расчеты онлайнДля удобства чтения и запоминания больших чисел цифры их разбивают на так называемые «классы»: справа отделяют три цифры (первый класс), затем еще три (второй класс) и т.д. Последний класс может иметь три, две и одну цифру. Между классами обычно оставляется небольшой пробел. Например, число 35461298 записывают так 35 461 298. Здесь 298 — первый класс, 461 — второй класс, 35 — третий. Каждая из цифр класса называется его разрядом; счет разрядов также идет справа. Например, в первом классе 298 цифра 8 составляет первый разряд, 9 — второй, 2 — третий. В последнем классе может быть три, два разряда (в нашем примере: 5 — первый разряд, 3 — второй) или один. Первый класс дает число единиц, второй — тысяч, третий — миллионов; сообразно с этим число 35 461 298 читается: тридцать пять миллионов четыреста шестьдесят одна тысяча двести девяносто восемь. Поэтому говорят, что единица второго класса есть тысяча; единица третьего класса — миллион. Таблица, Названия больших чисел
Единица четвертого класса называется миллиардом, или, иначе, биллионом (1 миллиард = 1000 миллионов). Единица пятого класса называется триллионом (1 триллион = 1000 биллионов или 1000 миллиардов). Единицы шестого, седьмого, восьмого и т.д. классов (каждая из которых в 1000 раз больше предшествующей) называются квадриллионом, квинтиллионом, секстиллионом, септиллионом и т.д. В помощь студенту
www.fxyz.ru Самое большое число в мире
“Я вижу скопления смутных чисел, которые скрывается там, в темноте, за небольшим пятном света, которое дает свеча разума. Они шепчутся друг с другом; сговариваясь кто знает о чем. Возможно, они нас не очень любят за захват их меньших братишек нашими умами. Или, возможно, они просто ведут однозначный числовой образ жизни, там, за пределами нашего понимания’’.Дуглас Рэй Продолжаем нашу рубрику САМОГО САМОГО. Сегодня у нас числа ... Каждого рано или поздно мучает вопрос, а какое же самое большое число. На вопрос ребенка можно ответить миллион. А что дальше? Триллион. А еще дальше? На самом деле, ответ на вопрос какие же самые большие числа прост. К самому большому числу просто стоит добавить единицу, как оно уже не будет самым большим. Процедуру эту можно продолжать до бесконечности. А если же задаться вопросом: какое самое большое число существует, и какое у него собственное название? Сейчас мы все узнаем ... Существуют две системы наименования чисел — американская и английская. Американская система постороена довольно просто. Все названия больших чисел строятся так: в начале идет латинское порядковое числительное, а в конце к ней добавляется суффикс -иллион. Исключение составляет название "миллион" которое является названием числа тысяча (лат. mille) и увеличительного суффикса -иллион (см. таблицу). Так получаются числа — триллион, квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион и дециллион. Американская система используется в США, Канаде, Франции и России. Узнать количество нулей в числе, записанном по американской системе, можно по простой формуле 3·x+3 (где x - латинское числительное).
Английская система наименования наиболее распространена в мире. Ей пользуются, например, в Великобритании и Испании, а также в большинстве бывших английских и испанских колоний. Названия чисел в этой системе строятся так: так: к латинскому числительному добавляют суффикс -иллион, следущее число (в 1000 раз большее) строится по принципу — то же самое латинское числительное, но суффикс — -иллиард. То есть после триллиона в английской системе идёт триллиард, а только затем квадриллион, за которым следует квадриллиард и т.д. Таким образом, квадриллион по английской и американской системам — это совсем разные числа! Узнать количество нулей в числе, записанном по английской системе и оканчивающегося суффиксом -иллион, можно по формуле 6·x+3 (где x - латинское числительное) и по формуле 6·x+6 для чисел, оканчивающихся на -иллиард.
Из английской системы в русский язык перешло только число миллиард (10 9), которое всё же было бы правильнее называть так, как его называют американцы — биллионом, так как у нас принята именно американская система. Но кто у нас в стране что-то делает по правилам! ;-) Кстати, иногда в русском языке употребляют и слово триллиард (можете сами в этом убедиться, запустив поиск в Гугле или Яндексе) и означает оно, судя по всему, 1000 триллионов, т.е. квадриллион. Кроме чисел, записанных при помощи латинских префиксов по американской или англйской системе, известны и так называемые внесистемные числа, т.е. числа, которые имеют свои собственные названия безо всяких латинских префиксов. Таких чисел существует несколько, но подробнее о них я расскажу чуть позже. Вернемся к записи при помощи латинских числительных. Казалось бы, что ими можно записывать числа до бессконечности, но это не совсем так. Сейчас объясню почему. Посмотрим для начала как называются числа от 1 до 10 33: И вот, теперь возникает вопрос, а что дальше. Что там за дециллионом? В принципе, можно, конечно же, при помощи объединения приставок породить такие монстры, как: андецилион, дуодециллион, тредециллион, кваттордециллион, квиндециллион, сексдециллион, септемдециллион, октодециллион и новемдециллион, но это уже будут составные названия, а нам были интересны именно собственные названия чисел. Поэтому собственных имён по этой системе, помимо указанных выше, ещё можно получить лишь всего три — вигинтиллион (от лат. viginti — двадцать), центиллион (от лат. centum — сто) и миллеиллион (от лат. mille — тысяча). Больше тысячи собственных названий для чисел у римлян не имелось (все числа больше тысячи у них были составными). Например, миллион (1 000 000) римляне называли decies centena milia, то есть "десять сотен тысяч". А теперь, собственно, таблица:
Таким образом, по подобной системе числа больше, чем 10 3003, у которого было бы собственное, несоставное название получить невозможно! Но тем не менее числа больше миллеиллиона известны — это те самые внесистемные числа. Расскажем, наконец-то, о них.
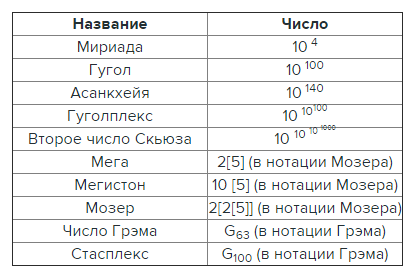
Самое маленькое такое число — это мириада (оно есть даже в словаре Даля), которое означает сотню сотен, то есть — 10 000. Слово это, правда, устарело и практически не используется, но любопытно, что широко используется слово "мириады", которое означает вовсе не определённое число, а бесчисленное, несчётное множество чего-либо. Считается, что слово мириада (англ. myriad) пришло в европейские языки из древнего Египта. Насчёт происхождения этого числа существуют разные мнения. Одни считают, что оно возникло в Египте, другие же полагают, что оно родилось лишь в Античной Греции. Как бы то ни было на самом деле, но известность мириада получила именно благодаря грекам. Мириада являлось названием для 10 000, а для чисел больше десяти тысяч названий не было. Однако в заметке "Псаммит" (т.е. исчисление песка) Архимед показал, как можно систематически строить и называть сколь угодно большие числа. В частности, размещая в маковом зерне 10 000 (мириада) песчинок, он находит, что во Вселенной (шар диаметром в мириаду диаметров Земли) поместилось бы (в наших обозначениях) не более чем 1063песчинок. Любопытно, что современные подсчеты количества атомов в видимой Вселенной приводят к числу 1067 (всего в мириаду раз больше). Названия чисел Архимед предложил такие:1 мириада = 104.1 ди-мириада = мириада мириад = 108.1 три-мириада = ди-мириада ди-мириад = 1016.1 тетра-мириада = три-мириада три-мириад = 1032.и т.д.
Гугол (от англ. googol) — это число десять в сотой степени, то есть единица со ста нулями. О "гуголе" впервые написал в 1938 году в статье "New Names in Mathematics" в январском номере журнала Scripta Mathematica американский математик Эдвард Каснер (Edward Kasner). По его словам, назвать "гуголом" большое число предложил его девятилетний племянник Милтон Сиротта (Milton Sirotta). Общеизвестным же это число стало благодаря, названной в честь него, поисковой машине Google. Обратите внимание, что "Google" — это торговая марка, а googol — число.
В интернете вы часто можете встретить упоминание, что Гугол самое большое число в мире - но это не так ... В известном буддийском трактате Джайна-сутры, относящегося к 100 г. до н.э., встречается число асанкхейя (от кит. асэнци — неисчислимый), равное 10 140. Считается, что этому числу равно количество космических циклов, необходимых для обретения нирваны.
Гуголплекс (англ. googolplex) - число также придуманное Каснером со своим племянником и означающее единицу с гуголом нулей, то есть 10 10100. Вот как сам Каснер описывает это "открытие": Words of wisdom are spoken by children at least as often as by scientists. The name "googol" was invented by a child (Dr. Kasner's nine-year-old nephew) who was asked to think up a name for a very big number, namely, 1 with a hundred zeros after it. He was very certain that this number was not infinite, and therefore equally certain that it had to have a name. At the same time that he suggested "googol" he gave a name for a still larger number: "Googolplex." A googolplex is much larger than a googol, but is still finite, as the inventor of the name was quick to point out. Mathematics and the Imagination (1940) by Kasner and James R. Newman. Еще большее, чем гуголплекс число — число Скьюза (Skewes' number) было предложено Скьюзом в 1933 году (Skewes. J. London Math. Soc. 8, 277-283, 1933.) при доказательстве гипотезы Риманна, касающейся простых чисел. Оно означает e в степени e в степениe в степени 79, то есть eee79. Позднее, Риел (te Riele, H. J. J. "On the Sign of the Difference П(x)-Li(x)." Math. Comput. 48, 323-328, 1987) свел число Скьюза к ee27/4, что приблизительно равно 8,185·10 370. Понятное дело, что раз значение числа Скьюза зависит от числа e, то оно не целое, поэтому рассматривать мы его не будем, иначе пришлось бы вспомнить другие ненатуральные числа — число пи, число e, и т.п.
Но надо заметить, что существует второе число Скьюза, которое в математике обозначается как Sk2, которое ещё больше, чем первое число Скьюза (Sk1). Второе число Скьюза, было введённо Дж. Скьюзом в той же статье для обозначения числа, для которого гипотеза Риманна не справедлива. Sk2 равно 101010103, то есть 1010101000 . Как вы понимаете чем больше в числе степеней, тем сложнее понять какое из чисел больше. Например, посмотрев на числа Скьюза, без специальных вычислений практически невозможно понять, какое из этих двух чисел больше. Таким образом, для сверхбольших чисел пользоваться степенями становится неудобно. Мало того, можно придумать такие числа (и они уже придуманы), когда степени степеней просто не влезают на страницу. Да, что на страницу! Они не влезут, даже в книгу, размером со всю Вселенную! В таком случае встаёт вопрос как же их записывать. Проблема, как вы понимаете разрешима, и математики разработали несколько принципов для записи таких чисел. Правда, каждый математик, кто задавался этой проблемой придумывал свой способ записи, что привело к существованию нескольких, не связанных друг с другом, способов для записи чисел — это нотации Кнута, Конвея, Стейнхауза и др. Рассмотрим нотацию Хьюго Стенхауза (H. Steinhaus. Mathematical Snapshots, 3rd edn. 1983), которая довольно проста. Стейн хауз предложил записывать большие числа внутри геометрических фигур — треугольника, квадрата и круга:
Стейнхауз придумал два новых сверхбольших числа. Он назвал число — Мега, а число — Мегистон. Математик Лео Мозер доработал нотацию Стенхауза, которая была ограничена тем, что если требовалаось записывать числа много больше мегистона, возникали трудности и неудобства, так как приходилось рисовать множество кругов один внутри другого. Мозер предложил после квадратов рисовать не круги, а пятиугольники, затем шестиугольники и так далее. Также он предложил формальную запись для этих многоугольников, чтобы можно было записывать числа, не рисуя сложных рисунков. Нотация Мозера выглядит так:
Таким образом, по нотации Мозера стейнхаузовский мега записывается как 2[5], а мегистон как 10[5]. Кроме того, Лео Мозер предложил называть многоугольник с числом сторон равным меге — мегагоном. И предложил число "2 в Мегагоне", то есть 2[2[5]]. Это число стало известным как число Мозера (Moser's number) или просто как мозер.
Но и мозер не самое большое число. Самым большим числом, когда-либо применявшимся в математическом доказательстве, является предельная величина, известная как число Грэма (Graham's number), впервые использованная в 1977 года в доказательстве одной оценки в теории Рамсея. Оно связано с бихроматическими гиперкубами и не может быть выражено без особой 64-уровневой системы специальных математических символов, введённых Кнутом в 1976 году. К сожалению, число записанное в нотации Кнута нельзя перевести в запись по системе Мозера. Поэтому придётся объяснить и эту систему. В принципе в ней тоже нет ничего сложного. Дональд Кнут (да, да, это тот самый Кнут, который написал "Искусство программирования" и создал редактор TeX) придумал понятие сверхстепень, которое предложил записывать стрелками, направленными в masterok.livejournal.com
chislitelnye.ru Занимательная статистика. Часть вторая, гигантскаяВ прошлом посте “занимательная статистика: от 1 и до 1 000 000” мы начали с 1 и постепенно добрались до 1 000 000, представляя числа в виде множества точек. Было здорово, но время развлечений прошло. Теперь все будет по-взрослому. Начнем с пока обозримых степеней числа 10. Степени числа 10 С числами от 1 до 1 000 000 степени не требовались: эти числа состояли из нескольких цифр, для умножения на 10 достаточно было добавить 0. Однако после миллиона нули множатся, как грибы после дождя, поэтому нам понадобится другая система обозначений — степени. Безумие, которое начнет из-за них происходить, называется экспоненциальным ростом. Например: результат умножения 9 845 625 675,438 на 8 372 745 993 275 будет все еще меньше 829. Когда речь заходит о по-настоящему гигантских числах, не менее значимым становится количество цифр в них. Для сокращения мы решили использовать степени числа 10, поскольку, к примеру, любое 70-значное число находится в промежутке между 1070 и 1071, чего вполне достаточно для его обозначения. К тому же так наглядно демонстрируется порядок величины чисел: каждая единица в значении степени увеличивает число в ее основании в 10 раз. Итак, начнем с того числа, на котором закончили в прошлый раз: 106 (1 миллион — 1,000,000) — Количество точек на той огромной картинке в конце предыдущего поста о цифрах. В зависимости от разрешения вашего монитора ее площадь составит около 0,81 м2 107 (10 миллионов) — В этом диапазоне находится число шагов, которое потребуется сделать, чтобы обойти вокруг Земли (40,000,000 шагов). Если каждый шаг представить в виде точки, как мы делали в прошлом посте, то все эти точки заполнят квадрат со стороной 6 метров. 108 (100 миллионов) — В категории сотен миллионов присутствует число книг, напечатанных за всю историю человечества (130 млн), и среднее количество слов, сказанных человеком в течение жизни (860 млн). В этой же области находятся шансы на выигрыш в крупные лотереи. Вероятность выигрыша в недавнем тираже американской лотереи Mega Millions равнялись 1 к 175,711,536. Во временной перспективе это число примерно равно количеству секунд в шести годах. Это как, зная, что ежик чихнет в ближайшие шесть лет всего один раз, поставить свои кровно заработанные на какую-то конкретную секунду — скажем, на 02:52:36 19 марта 2017 года. И выиграть только в случае, если в эту самую секунду ему и случится чихнуть. Ну, вы поняли про лотереи. 109 (1 миллиард — 1,000,000,000) — Среди единиц миллиардов мы найдем число секунд в столетии (около 3,000,000,000), количество людей на планете (7,125,000,000). Миллиард точек покроет площадь двух баскетбольных площадок. 1010 (10 миллиардов) — Здесь соседствуют интересные числа: количество лет с момента Большого взрыва (13,7 млрд) и количество секунд с момента появления Христа (60 млрд). 1011 (100 миллиардов) — Количество звезд Млечного пути и число галактик в наблюдаемой вселенной (100-400 млрд). Так что случись компьютеру перечислять видимые галактики по одной в секунду с момента появления Христа, он и сейчас был бы далек от окончания списка. 1012 (1 триллион — 1,000,000,000,000) — Миллион миллионов. Отметка на шкале весов в фунтах, если поставить на них всех живущих (~1 трлн), время существования человечества в секундах (~100,000 лет = ~3 трлн секунд) и превышающее сумму двух предыдущих количество миль в одном световом годе (6 трлн). Триллион — это настолько много, что потребуется всего 4 триллиона миллиметров ленты, чтобы завязать бантик вокруг солнца. 1013 (10 триллионов) — Пожалуй, это одно из самых больших чисел, которое можно услышать в обычном разговоре — например, номинальный ВВП США в 2013 году составил 17 триллионов, а текущий долг — почти 18 триллионов. Оба этих числа теряются на фоне количества клеток в человеческом теле (37 трлн). 1014 (100 триллионов) — Примерно столько букв содержится во всех напечатанных книгах, и оно же равно числу бактерий в человеческом организме. Также в диапазоне сотен миллиардов находятся все деньги мира ($241 трлн, как уже упоминалось в предыдущем посте о цифрах). 1015 (1 квадриллион) — Ну вот, прощайте, нормальные слова. «Миллион», «биллион» и даже «триллион» часто употребляемы. Но никто не говорит «квадриллион». Иногда вместо него употребляют «миллион миллиардов». Как бы его ни называли, на Земле водится квадриллион муравьев. Сопоставив это число и предыдущий факт о бактериях, получим весьма яркий, хоть и несимпатичный образ — каждый десятый муравей планеты бегает внутри вашего тела. 1016 (10 квадриллионов) — Количество игральных карт, которыми можно покрыть поверхность планеты (89 квадриллионов). От такого количества сброшенных карт ваши партнеры по бриджу будут вне себя. 1017 (100 квадриллионов) — Число секунд с момента Большого Взрыва. 1018 (1 квинтиллион) — Aka миллиард миллиардов. Квинтиллион звучит еще более несуразно, чем квадриллион. Это слово можно услышать только от человека с серьезными проблемами с социализацией. И тем не менее, это вся вода мирового океана в кубометрах и число атомов в одной крупице соли (1,2 квинтиллиона). Песчинок на всех пляжах мира 7,5 квинтиллионов. Столько же, сколько атомов в 6 крупицах соли. 1019 (10 квинтиллионов) — Расстояние в миллиметрах от вашего компьютера до ближайшей звезды (38 квинтиллионов). 1020 (100 квинтиллионов) — Столько метровых шагов потребуется, чтобы пройти весь Млечный путь. Вы знакомы с понятием «объем Планка»? Это наименьшая единица объема, используемая учеными. Настолько маленькая, что 100 квинтиллионов объема Планка не превышают размера протона(!). Подробнее об этой единице измерения мы поговорим позже. Кстати, о точках: картинкой с 600 квинтиллионами точек можно полностью покрыть поверхность Земли. 1021 (1 секстиллион) — Это уже находится полностью вне лексикона. Вы когда-нибудь слышали это слово, произнесенным вслух? Может, это и неплохо? 1023 (100 секстиллионов) — По самым приблизительным оценкам, число звезд в наблюдаемой вселенной. Также это число встречалось нам в школе на уроках физики: 602 секстиллиона или 6,02 x 1023 — число Авогадро, молярный объем газа. А еще это количество атомов в одном грамме водорода. 1024 (1 септиллион) — Триллион триллионов. Земля весит около 6 септиллионов килограмм. 1025 (10 септиллионов) — Число капель воды в Мировом океане. 1027 (1 октиллион) — Если бы Земля была полым шаром, 1 октиллион горошинок заполнил бы его полностью. А теперь нас ждет гигантский скачок туда, где размеры нашей планеты станут просто крошечными , а Большой Взрыв — самый частый участник событий. Уровень этих чисел демонстрирует только сама наблюдаемая вселенная — сфера диаметром около 92 миллиардов световых лет. 1080— Чтобы получить 1080, умножьте триллион на триллион, потом еще на триллион, потом ещё раз, ещё и ещё, а затем на сто миллионов. И вот перед вами общая оценка числа атомов во вселенной. 1086 — А как насчет набить вселенную горохом? Для этого потребуется 1086 горошин. 1090 — А это количество песчинок среднего размера (0,5 мм в диаметре), которое заполнит вселенную целиком. Гугол — 10100 Название «гугол» появилось в 1938 году, когда одним прекрасным днем американский математик Эдвард Казнер попросил своего 9-летнего племянника Милтона придумать имя для числа 10100 — единицы со ста нулями. Малыш предложил «гугол». Казнер, вероятно, счел этот ответ разумным, согласился, да так его и оставили. 59 лет спустя Сергей Брин и Ларри Пейдж дали такое же имя своей новой поисковой системе. Они хотели подчеркнуть колоссальность объемов информации, с которыми она будет работать. А ошибка в написании названия была допущена случайно (английское название гугола — googol — прим. переводчика). Гугол — это сколько? Вновь представьте вселенную, заполненную песчинками — десятки миллиардов световых лет от Земли в любом направлении — повсюду песок. Триллионы лет можно лететь на полной скорости через весь этот песок и так и не достичь края. Много, очень много песка. Теперь представьте, что остановив корабль, достаете одну из песчинок и рассматриваете её под микроскопом. И в многократном увеличении видите, это не целая песчинка, а 10 миллиардов микроcкопических гранул,составляющих эту песчинку. Так вот, если представить, что каждая из песчинок, заполнивших вселенную состоит из 10 миллиардов крошечных частиц, то суммарное число микроскопических частиц и будет гугол. Мы уже, казалось бы, использовали все мельчайшие и колоссально большие примеры из физического мира для демонстрации чисел. Хотя нет, вот еще три: 10113— Число атомов водорода, которыми можно заполнить вселенную. 10122— Число протонов, которыми также можно заполнить вселенную целиком. Если вдруг у вас закончится водород. 10185— Вернемся к объему Планка (мельчайшая единица объема). Сколько этих мельчайших единиц может поместиться в грандиознейшем объеме — наблюдаемой вселенной? 10185. И в этом примере мы абсолютно точно достигли малого и большого экстремумов физического мира. Гуголплекс — 10гугол После популяризации гугола, Казнер едва ли мог удержаться и не повторить этот фокус — он попросил племянника выдумать новый термин. Он едва успел закончить просьбу, как Милтон выпалил: «гуголплекс». И в характерной для ребенка манере описал это число как «единицу, после которой пишете нули, пока не надоест». С этим описанием Казнер, к счастью, не согласился и дал числу настоящее определение: 10гугол или 1 с гуголом нулей. С написанным полностью показателем степени гуголплекс выглядит так: 1010,000,000,000,000,000,000,000,000.,000,000,000,000,000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000,000,000,000 Гугол — единица со ста нулями, в десять миллиардов раз больше количества песчинок, которое заполнит вселенную. Можно ли вообразить число с гуголом нулей после единицы? Представить это число невозможно, в наших силах лишь представить, сколько времени займет его записывание. Выше указана всего лишь степень, а собственно число — это записывание гугола нулей. Для начала стоит найти такую площадь. Как мы помним, вселенная, доверху заполненная песком — это лишь одна десятимиллиардная гугола, значит, все, что нам осталось сделать — это, обзаведясь супермаленькой ручкой, на каждой песчинке написать 10 миллиардов микроскопических нулей. И когда мы это сделаем, гуголплекс будет записан. Сколько это займет? По наблюдениям ученых человек способен разборчиво написать 36 нулей за 10 секунд. Исходя из этой оценки, если бы человек делал это по 16 часов каждый божий день, за 80 лет он бы исписал только половину песчинки. На целую потребуется время протяженностью в две человеческие жизни. Всего на Земле существовало около 107 миллиардов людей. Если бы каждый из них посвятил всю свою жизнь написанию нулей на песчинках, сейчас мы бы уже наполнили песчинками с нулями куб со стороной 1,7 метра. И всё. И все же получить представление о размере числа можно. Все возможные квантумные состояния, возникающие в пространстве, составляющем одного человека, все равно меньше гуголплекса. А означает это, что согласно теории вероятности, во вселенной объемом в гуголплекс кубических метров (пространстве исключительно огромных размеров) будут точные копии любого читающего эту статью. Дело в том, что во вселенной подобных размеров все возможные сочетания атомов в составе одного человека с большой вероятностью повторятся много раз, а значит, случится и несколько копий каждого из нас. Включая точную копию, но с кошачьими усами, или копию кукольного роста или с крыльями и шестью пальцами. И это не фантастика, это реальность огромных вселенных. Число Грехема Не будем приводить здесь определение числа Грехема, поскольку оно очень сложное и запутанное. Скажем лишь, что оно является верхней границей для решения определенной математической проблемы и названо в честь американского математика Рональда Грехема. Грехем вывел это число в 1977 году, широкой публике оно стало известно после того, как коллега Грехема описал его в журнале «Scientific American» как «границу настолько большую, что ей принадлежит рекорд как наибольшему числу, когда-либо использовавшемуся в серьёзном математическом доказательстве». В 1980 году число попало в Книгу рекордов Гиннесса по той же причине, и несмотря на то, что на сегодняшний день этот рекорд побит, до сих пор остается самым большим числом, известным большому количеству людей. Число Грехема в невообразимое количество раз больше, чем гугол и даже гуголплекс. На самом деле вся наблюдаемая вселенная слишком мала для того, чтобы вместить в себя обыкновенную десятичную запись числа Грехема. Для восприятия и операций с числами такого порядка существуют специальные алгоритмы, точнее, один алгоритм: гипероператор. Последовательность гипероператоров — это серии математических операций (например,сложение, умножение и т. д.), в которых каждая следующая операция в последовательности определяется через предыдущую, повторенную n раз. Вы быстро все поймете. Начнем с первой и самой простой операции: счета. Операция нулевого уровня — Счет Последовательный счет. Простая операция. Пример: дано число 3, для получения искомого числа перечисляется последовательность 3,4,5,6,7 и т. д. Операция первого уровня — Сложение Сложение — операция следующего, боле высокого уровня по сравнению со счетом, «сокращенный счет». Вместо перечисления 3,4,5,6,7, можно сложить 3+4 и перейти прямо к 7. Сложение сокращает операции счета в одно, более короткое действие. Операция второго уровня — Умножение Снова на уровень выше, умножение — это сокращенное сложение. Вместо перечисления 3+3+3+3 умножение позволяет сократить операции сложения до одного действия более высокого уровня умножения 3х4. Результатом умножения являются гораздо большие числа: при сложении двух 8-значных чисел суммой будет 8— или 9-значное число, а при умножении — 15— или 16-значное. Операция третьего уровня — Возведение в степень (↑) Следующий уровень — возведение в степень — это сокращенное умножение. Вместо перечисления 3х3х3х3 возведение в степень позволяет сократить операции умножения до одного действия — 34. Для большинства людей возведение в степень — последний, самый высокий уровень гипероператора, который они используют. Но ключ к действительно большим числам в применении гипероператоров следующих уровней. Для этого нам потребуется другой вид обозначений. Собственно, каждый уровень различался символом (+,х, степень), но поскольку уровней много, не стоит продолжать вводить для каждого свой символ. Мы воспользуемся стрелочной нотацией Кнута, позволяющей использовать один символ на каждом уровне. Стрелочная нотация Кнута применяется в операциях третьего уровня и заменяет степень одной стрелкой — ↑. Таким образом, вместо обозначения 34 мы используем 3 ↑ 4, но сама операция возведения в степень останется неизменной. 3 ↑ 4 = 81 2 ↑ 3 = 8 5 ↑ 5 = 3125 1 ↑ 38 = 1 Теперь двинемся дальше и, наконец, увидим волшебство гипероператоров: Операция четвертого уровня — Тетрация (↑↑) Тетрация — сокращенное возведение в степень. Перед тем как начать разбираться в сокращении действий в строке степени, нужно разобраться, что это строка обозначает. Прежде мы производили одно вычисление — число в основании возводили в степень в ее показателе, а что если увеличить количество степеней: Мы получили степенную башню, в которой возведение в степень начинается с самых верхних уровней к начальному. Таким образом, Пока ничего особо впечатляющего, но взгляните сюда: Используем скобки, чтобы выделить этапы вычисления степени: число, содержащее 3,6 триллиона цифр. Помните, гугол и его микроскопические частицы песка, наполнившего вселенную? Так вот это число, состоящее лишь из 100 цифр. Степенная башня из 4 уровней с основанием 3 превосходит не только гугол, но 10185, число объемов Планка во вселенной, максимальное число физического мира. Гуголплекс пока все же больше, но это легко изменить, добавив еще одну 3 в степень. = 3 число, содержащее 3,6 триллиона цифр Это число уже в разы больше гуголплекса, который всего лишь 10 число, содержащее 100 цифр. Кстати, с помощью степенной башни можно записать гуголплекс гораздо короче: или так Можете представить, какие гигантские числа позволяют вычислить высокие степенные башни. Тетрация в действии. Степенные башни можно представить и с помощью стрелок Кнута, но для отличия уровней башни от одинарной степени будем использовать двойные стрелки. равно 3 ↑ (3 ↑ (3 ↑ 3)). А теперь сократим 4 одинарные степени в выражение 3 ↑↑ 4. Аналогично 3 ↑↑ 5 = 3 ↑ (3 ↑ (3 ↑ (3 ↑ 3))) = 4 ↑↑ 7 = 4 ↑ (4 ↑ (4 ↑ (4 ↑ (4 ↑ (4 ↑ 4))))) = степенная башня из 7 уровней с основанием 4. Общее правило: Тетрация (операция 4 уровня). Выражение a↑↑b означает степенную башню с b количеством уровней и основанием a. Перед переходом к следующему, более сложному гипероператору убедитесь, что усвоили теорию и обозначения тетрации. Операция пятого уровня — Пентация (↑↑↑) Пентация — это повторяющаяся тетрация, объединяет последовательности с двумя стрелками в одну операцию. Гипероператор каждого последующего уровня сокращает последовательность предыдущего уровня, используя термин b для обозначения длины последовательности. Например: Умножение сокращает последовательность сложения. Возведение сокращает последовательность умножения. Тетрация сокращает последовательность возведения в степень. В каждом случае a — число в основании, b — длина последовательности. Но что же сокращает пентация? Принцип работы этого гипероператора можно описать как «безумное поглощение степенных башен». Представьте последовательность степенных башен в определенном порядке. Все они имеют одинаковое число в основании, отличаются только количеством уровней. Вычисляем результат первой степенной башни и подставляем его вместо значения высоты (количества уровней) для следующей башни. Затем вычисляем и ее результат и подставляем его в количество уровней следующей степенной башни. И так далее. Каждая последующая башня «поглощает» результат предыдущей, используя её результат для собственного «безумного» роста. Вот почему это происходит: 3 ↑↑↑ 4 означает последовательность 4-х операций вида (3 ↑↑ 3). Таким образом: 3 ↑↑↑ 4 = 3 ↑↑ (3 ↑↑ (3 ↑↑ 3)) Помните, символ ↑↑ обозначает последовательность возведения в степень с количеством уровней b, следовательно Из предыдущих вычислений вы, должно быть помните, что а следовательно Таким образом результат решения первой степенной башни из 3 уровней превышает 7 триллионов. Используем этот результат как количество уровней второй степенной башни и получаем выражение (3 ↑↑ 7,625,597,484,987). Представляете, какой высоты будет башня с более чем 7 триллионами уровней степеней? Если каждая 3 будет размером в 2 сантиметра, высота степенной башни составит 150 миллионов километров, и она дорастет до солнца. И даже если мы используем крошечные цифры 3, по 2 мм каждая, длина нашей башни 40 раз покроет расстояние до Луны и обратно. И обернет Землю 400 раз. Назовем её для краткости «башней солнца», в пером варианте она даже достает до него. Вернемся к нашим расчетам: =3↑↑(«башня солнца») Последняя операция — 3↑↑(«башня солнца») — будет представлена степенной башней с количеством уровней, которые мы узнаем лишь вычислив результат «солнечной» башни. И в высоту она уже не поместится в пределах наблюдаемой вселенной. И пока мы не вычислим результат этой последней «вневселенской» башни, мы не узнаем результат пентации 3 ↑↑↑ 4. Пентация (использующая обозначение ↑↑↑) — это «поглощение» степенной башней результата предыдущей, при котором количество уровней в каждой последующей становится все более непостижимым, не говоря уже о конечном числе. Пентация (операция 5 уровня). Выражение a↑↑↑b означает «безумное поглощение» степенных башен с b количеством степенных башен и основанием a. Каждое выражение в скобках — степенная башня, результат решения которой занимает позицию b в предыдущих скобках— становится значением количества уровней для предыдущей степенной башни. «Безумное поглощение» степенных башен. Первая башня в основании формулы имеет a уровней. Результат решения этой степенной башни «поглощается» предыдущей башней и становится количеством её уровней и т. д. Операция шестого уровня — Гексация (↑↑↑↑) Гипероператор шестого уровня — гексация, она же повторенная пентация. Это уже не поглощение башен, это просто праздник обжорства. Выглядит это так: «Поглощение» башен дошло до финального числового результата. Это число становится количеством башен в следующем «поглощении», которое также в результате получает уже абсолютно невероятное число… и так далее. 3 ↑↑↑↑ 4 — пример гексации, в которую входят 3 полных ↑↑↑-пентаций-поглощений, каждая из которых сообщает своим результатом количество степенных башен в следующей: 3 ↑↑↑↑ 4 = 3 ↑↑↑ (3 ↑↑↑ (3 ↑↑↑ 3)) Помните, выражение 3 ↑↑↑ 3 имеет результатом «башню солнца». Таким образом: 3 ↑↑↑↑ 4 = 3 ↑↑↑ (3 ↑↑↑ (3 ↑↑↑ 3)) = 3 ↑↑↑ (3 ↑↑↑ («башня солнца»)) Поскольку символ ↑↑↑ означает тентацию и «поглощение» башен, результат выражения 3 ↑↑↑ («башня солнца») станет число, которое протянется в пару соседних галактик. И по принципу «поглощения» это число станет количеством башен в следующей тентации. Когда будет решена и она, мы получим результат начальной гексации. Наглядное объяснение гексации: Гексация (операция 6 уровня).Выражение a↑↑↑↑b означает «суперпоглощение» степенных башен с b количеством степенных башен и основанием a. Каждое выражение в скобках — пентация, «поглощение» нескольких башен, результат решения которой занимает позицию b в предыдущих скобках— становится значением количества башен для предыдущей серии «поглощений». «Суперпоглощение». Первая пентация-«поглощение» (крайняя правая) стартует с a количества башен, результат решения станет количеством башен в следующей серии «поглощений» и т. д. Финальный результат последней серии «поглощений» станет результатом гексации. Так, собственно, и работает серия гипероператоров. Вы можете продолжить увеличивать количество стрелок, каждый раз приумножая возможности в вычислении суперогромных чисел. Мы познакомились с семью уровнями гиперопераций, включая первые 4 со стрелками: ↑ = возведение в степень ↑↑ = степенная башня ↑↑↑ = тентация-«поглощение» ↑↑↑↑ = гексация-«суперпоглощение» Теперь в ваших руках все необходимые инструменты, чтобы познакомиться с числом Грехема: Число Грехема равно термину g64. До него мы еще доберемся, сначала разобравшись с числом g1. g1 = 3 ↑↑↑↑ 3 Гексация, её мы уже знаем, ну вроде как. Приступаем к решению. Вот как оно будет выглядеть: Гексация g1. (b-1) — две серии «поглощений» в этой гексации. Результат вычислений этой башни станет количеством уровней в башне, расположенной выше. Башня солнца. результат вычислений этой башни станет количеством башен в левой серии «поглощений». Три точки будут заменены безумным числом башен — оно будет больше числа Планковских объемов во вселенной. Раскладываем на составляющие g1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) и получаем две тетрации-«поглощения». Начнем с первой, обведенной на рисунке красным: g1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑↑ (3 ↑↑ (3 ↑↑ 3)) Первая серия «поглощений» состоит из двух степенных башен. Первая башня — очень простая, поскольку уровней в ней всего 3: Мы помним, что 333 = 7,625,597,484,987, следовательно Мы знаем, что результатом выражения (3 ↑↑ 7,625,597,484,987) будет наша «башня солнца»: Вкратце: g1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑↑ (башня солнца) Две первые серии «поглощений» выдали невероятно огромное число «башни солнца». Помните, прежде мы уже изучили, как быстро нарастают числа в степенной башне:, число гораздо большее, чем гугол, будучи написанным, обернет землю пару сотен раз. — не говоря уже о числе в степени, состоящей из 3,6 триллиона цифр. Числе, превосходящем гуголплекс, числе, записать которое не хватит места во всей наблюдаемой вселенной. Выглядит безумно, правда? И это только лишь несколько сантиметров «башни солнца». А на расстоянии метра числа станут гораздо, гораздо больше, чем можно себе представить. Все лишь на расстоянии метра башни высотой в 150 миллионов километров. Результат решения степенной башни высотой до солнца можно смело называть безумным. Поскольку будучи не в состоянии осознать цифры, возникающие на первых уровнях башни, мы можем смело называть безумными те, что находятся на расстоянии в 150,000,000 км. Вернемся к нашему решению: g1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑↑ (башня солнца) И заменим «башню солнца» на результат: g1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑↑ (башня солнца) = 3 ↑↑↑ безумное число Теперь, мы можем перейти ко второй тетрации. В ней будет безумное число башен. Это число настолько велико, что его даже не объяснить. По сравнению с ним объемы Планка во вселенной — детские забавы, гуголплекс смехотворен. И это количество степенных башен во второй тетрации. Итак, дано безумное число башен, понемногу, одну за другой, мы будем вычислять результат и подставлять его в количество уровней следующей башни, и снова вычислять результат… И так безумное число раз. Пока наконец не дойдет до окончательной цифры, которая станет решением гексации 3 ↑↑↑↑ 3. И это число будет g1 aka просто невозможное. Дальше надо добраться до g2. Вот как мы это сделаем: Смотрите на схему на рисунке, пока не поймете, насколько все непросто. Теперь продолжим. Да, мы полдня продирались от одной стрелки к четырем, справляясь с трудностями каждого нового уровня, осваивая невероятные возможности каждого следующего гипероператора. И подошли к просто невозможному числу g1. Грехем решил повторить с g2 тот же фокус, что он проделал с g1, с той лишь разницей, что вместо стрелок вместо 4 будет просто невозможному числу. «Безумное поглощение», но не башен, а стрелок. Число g1 станет количеством СТРЕЛОК в формуле g2. Кажется, голова взорвется от следующего уровня — пяти стрелок, но в g2 их не пять, а гораздо больше, больше, чем Планковских объемов во вселенной, больше гуголплекса. И это уровень гипероператора, используемого g2. Число Грэхэма возводит в степень само понятие возведения в степень. Разумеется, мы даже не будем пытаться вывести число g2, а без этого мы мало что можем о нем рассказать. А g3 и прочие, спросите вы. Рассчитанное до натурального число g2 станет количеством стрелок в формуле g3, результат которого в свою очередь станет основой для расчета g4 и так далее до g64. Наглядно число Грехема выглядит так: Высоких и измеримых вам конверсий! По материалам: waitbutwhy.com, image source Maryam 10-12-2014 lpgenerator.ru Пако Рабан миллион "Paco Rabanne 1 million"В связи с участившимся производством подделок, велика вероятность покупки поддельного товара. К сожалению, от этого не застрахован никто. Но можно существенно уменьшить вероятность приобретения копии, если быть предельно внимательным при выборе, заранее изучить отличия оригинала от подделки. На примере туалетной воды Paco Rabanne 1 million попробуем разобраться, как должен выглядеть оригинальный флакон и как уберечь себя от поддельного продукта. Paco Rabanne 1 million — упаковкаЛюбая коробка, в которой находится флакончик духов упакована в пленку. Здесь можно увидеть первое отличие. Пленка оригинала плотная, качественная, тогда как у копии слюда тонка, быстро мнется.
Цвет коробок тоже может заметно отличаться, что хорошо видно на фото. Шрифт, у настоящей упаковки, более тонкий.
Как видно на следующем фото, отличия тут видны явно. Отсутствие у коробки Пако Рабан миллион защитного кода, говорит о том, что перед вами подделка. Также заметно отсутствие или искажение значимых надписей.
На оборотной стороне коробочки присутствует информация о составе продукта и его происхождении. У оригинального Пако Рабан миллион буквы напечатаны определенным шрифтом, блоки расположены в четкой последовательности в нижней части, чего не скажешь о копии.
ФлаконPaco Rabanne 1 million мужские известны своим уникальным флаконом. В варианте оригинала флакончик гладкий, отсутствуют вмятины и царапины. У реплики надпись с названием марки вдавлена глубже, нанесена небрежно.
Оригинальный пузырек по длине меньше поддельного.
На верхней части видно как сильно отличаются флаконы. Низкое качество покраски, щели между элементами и их грубая обработка — отличительные признаки контрафакта.
У оригинального Пако Рабан миллион пластик очень хорошего качества.
На дне пузырька настоящего Paco Rabanne 1 million выбита перевернутая цифра «5», у реплики вы это не увидите.
Зазоры на флаконе и цвет жидкости выдают реплику.
Батч-кодУникальный серийный номер должен присутствовать на флакончике, упаковке и должен быть одинаков. У подделки их либо нет, либо они различаются.
Невозможно на 100% отгородить себя от покупки копии, но рассмотрев характерные отличия истинного Paco Rabanne 1 million мужские от низкокачественной реплики возможность наслаждаться подлинным ароматом увеличивается.
Что ещё почитать: chanelmademoiselle.ru Системы наименования чисел - это... Что такое Системы наименования чисел?В европейской традиции исторически сложились два варианта построения системы наименования чисел. Краткая историяТермин «миллион» итальянского происхождения и встречается уже в первой печатной арифметике (анонимной), вышедшей в итальянском городе Тревизо в 1478 году, и ещё ранее в нематематической книге путешественника Марко Поло (умер в 1324 году), а в форме «миллио» — уже в рукописи 1250 года. В рукописи французского математика Шюке (умер около 1500 года), напечатанной в 1880 году, впервые появляются термины «биллион» — 1012, «триллион» — 1018 и дальнейшие; в печатном руководстве биллион в значении 1012 появляется в 1602 году. Слово «миллиард», имевшее вначале значение 1012, получило значение 109 (тысячи миллионов) в «Арифметике» Траншана (1558) и употреблялось во Франции в XIX веке наравне со словом «биллион». В Германии это слово вошло в употребление лишь после получения от Франции 5 миллиардов контрибуции после франко-прусской войны 1871 года. Для чтения многозначных чисел анонимная рукопись 1200 года впервые рекомендует разбить цифры на группы по 3 или отмечать группы точками вверху или дугами; это же затем рекомендует Леонардо Пизанский (1228). К этой системе приходят и последующие авторы. Использование систем наименования чисел в мире:
В России первоначально была введена система наименования чисел с длинной шкалой, и, по-видимому, в печатном виде впервые в 1703 году в «Арифметике» Л. Ф. Магницкого. Однако в конце XVIII века, в царствование императора Павла I, вслед за Францией произошёл переход на короткую шкалу. Так, в опубликованном в 1798 году переводе части первой — «Арифметика» — «Курса математики» Этьенна Безу введена система наименования чисел с короткой шкалой, при том, что ещё в опубликованной в 1791 году книге «Арифметика или числовник» Н. Г. Курганова (1725 или 1726—1796) используется длинная шкала. В дальнейшем выбор системы наименования чисел в России — СССР — РФ не менялся. Однако Франция в 1948 году вернулась к системе с длинной шкалой, поэтому сейчас используемая в России система отличается от французской, хотя и заимствовалась во Франции. Короткая шкалаВ случае короткой шкалы все названия больших чисел строятся так: в начале идёт латинское числительное[1], а в конце к нему добавляется суффикс «-иллион». Исключение составляет название «миллион», которое образовано от латинского существительного mille «тысяча» при помощи увеличительного суффикса «-иллион». Так получаются числа — миллион, биллион[2], триллион, квадриллион, квинтиллион, секстиллион и т. д. Система наименования чисел с короткой шкалой используется в России, США, Канаде, Великобритании, Греции и Турции. Количество нулей в числе, записанном по этой системе, определяется по формуле 3·x+3 (где x — латинское числительное). Длинная шкалаНазвания чисел в этой системе строятся так: к латинскому числительному[1] добавляют суффикс «-иллион», название следующего числа (в 1000 раз большего) образуется из того же самого латинского числительного, но с суффиксом «-иллиард». То есть после триллиона в этой системе идёт триллиард, а только затем квадриллион, за которым следует квадриллиард и т. д. Количество нулей в числе, записанном по этой системе и оканчивающегося суффиксом «-иллион», определяется по формуле 6·x (где x — латинское числительное) и по формуле 6·x+3 для чисел, оканчивающихся на «-иллиард». Сравнение системТаблица от значения к названию
Таблица от названия к значениюПримечания
Литература
dic.academic.ru
|











 Эдвард Каснер (Edward Kasner).
Эдвард Каснер (Edward Kasner).