|
|
|
|
|
|
|
|
|
|
Геодезия: весь мир на карте! Карта геодезияГеодезические основы карт лекцииКАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ Факультет географии и экологии Кафедра физической и экономической географии Учебно-методическоепособие по курсу ГЕОДЕЗИЧЕСКИЕ ОСНОВЫ КАРТ Казанский федеральный университет УДК 528.23 Печатается по решению Редакционно-издательскогосовета ФГАОУВПО«Казанский(Приволжский) федеральный университет» Учебно-методическойкомиссии факультета географии и экологии КФУ Протокол №1 от26 января2011 г. Заседания кафедры физической и экономической географии Протокол № от г. Составители: асс. М.В. Рожко, доц. Г.Н. Булатова Научный редактор проф. В.А. Рубцов Рецензент доц. В.В. Мозжерин Геодезические основы карт: Учебно-методическоепособие по курсу/ М.В. Рожко, Г.Н. Булатова. – Казань: Казанский федеральный университет, 2011. – 35 с. В учебно-методическомпособии представлена программа лекционного курса«Геодезические основы карт», даны краткие теоретические сведения по основным темам, представлены планы практических и семинарского занятий, перечень основных понятий и определений по курсу, вопросы для самоконтроля и экзаменационные вопросы, а также список литературы. Издание предназначено для студентов изучающих дисциплину «Геодезические основы карт». © Казанский университет, 2010 ВВЕДЕНИЕ Карты используются человечеством многие века. Они необходимы для решения многих практических задач. Карты используются в научных, образовательных целях, в военном деле, в туризме, при анализе, планировании, проектировании и для многих других нужд. Не уменьшается значение карт и в условиях развития геоинформационных технологий. Одной из главных особенностей географических карт является их математически определенное построение. Оно достигается, в том числе путем опоры на геодезическую основу карт. Геодезическая основа карты - совокупность геодезических данных, необходимых для создания карты и определяющих положение объектов на карте по широте, долготе и абсолютной высоте. Данное учебно-методическоепособие предназначено для студентов, изучающих курс«Геодезические основы карт». В нем представлены планы практических и семинарского занятий, методические указания к ним. Пособие может использоваться в качестве дополнительного источника информации для подготовки к экзамену по курсу, так как в нем даны краткие теоретические сведения по основным темам и основные понятия и определения. Цель курса «Геодезические основы карт» - ознакомление студентов с геодезическими основами карт, как необходимой основой для картографирования, с формой и размерами Земли, историей изменения представлений о ней, эллипсоидами вращения, как математически принятой формой Земли, с понятием координат, их видами, способами их определения. Задачи курса состоят в том, что студенты, завершившие изучение данной дисциплины должны: -понимать важность геодезических основ в картографировании, понимать значение основных определений; -обладать теоретическими знаниями о фигуре и размерах Земли, -ориентироваться в видах координат; -приобрести навыки по работе с различными видами координат. 1. ТЕМАТИЧЕСКИЙ ПЛАН ЛЕКЦИЙ ТЕМА 1. ВВЕДЕНИЕ. ОБЩАЯ ХАРАКТЕРИСТИКА ГЕОДЕЗИЧЕСКИХ ОСНОВ КАРТ. В вводной части дается определение геодезических основ карт. Указываются цели курса, структура курса. Дается структура геодезических основ карт(т.е. картографические основы, которые являются геодезическими): форма и размеры Земли, координаты. Даются основные определения: геодезия, карта, картографические проекции и др. ТЕМА 2. ФИГУРА И РАЗМЕРЫ ЗЕМЛИ. Изучение фигуры Земли как древнейшая научная проблема естествознания. Идея о шарообразности Земли. Античные доказательства о шарообразности Земли. Земля– сфера. «Математические начала натуральной философии» И.Ньютона. Экспедиции в Перу и Лапландию. Метод триангуляции. Градусные измерения в России. Открытие А.Клеро связи ускорения силы тяжести с широтой места. Гравиметрический метод. Физическая или топографическая поверхность. Уровенная поверхность. Геоид. Квазигеоид. Эллипсоид вращения. Общеземной эллипсоид. Референц- эллипсоид. Уклонение отвесной линии. Эллипсоид Крассовского. Использованиереференц-эллипсоидовв разных странах: эллипсоиды Бесселя, Хейфорда, Кларка, Эвереста, Австралийский, Вальбека, Деламбера, WGS-84, ПЗ-90 и др. ТЕМА 3. ПОНЯТИЕ О ГЕОДЕЗИЧЕСКИХ СЕТЯХ. Понятие геодезическая сеть. Опорные пункты. Астрономический способ. Геодезический способ. Спутниковый способ. Классификация геодезических сетей. Государственные плановые сети. Метод триангуляции. Метод полигонометрии. Метод трилатерации. Связь пунктов геодезических сетей различных материков. Синхронный метод. Орбитальный метод. Применение радиогеодезии. Метод пересечения створа. ТЕМА 4. ЗАМЕНА ЭЛЛИПСОИДА ШАРОМ. ОТОБРАЖЕНИЕ ШАРА НА ШАР. Актуальность замены эллипсоида шаром. Сферическое отображение. Равноугольное отображение. Равновеликое отображение. Равнопромежуточное отображение. Проектирование с сохранением длин меридианов. Проектирование с сохранением длин параллелей. Отображение шара на шар. Способ Гильберта. ТЕМА 5. КООРДИНАТНАЯ СИСТЕМА. Общие понятия о системах отсчета. Понятие координаты. Понятие координатная система. Общеземная координатная система. Модель планеты Земля. Ориентирование пространственной прямоугольной системы координат в теле Земли. Референцные координатные системы. Система координат1942 года. Система координат1995 года. ТЕМА 6. ГЕОГРАФИЧЕСКИЕ КООРДИНАТЫ. Понятие географические координаты. Долгота. Широта. Меридиан. Параллель. Астрономические координаты. Плоскость астрономического меридиана. Астрономическая широта. Астрономическая долгота. Геодезические координаты. Плоскость геодезического меридиана. Геодезическая широта. Геодезическая долгота. ТЕМА 7. ПЕРЕХОД ОТ РЕАЛЬНОЙ(ФИЗИЧЕСКОЙ) ЗЕМНОЙ ПОВЕРХНОСТИ К ПОВЕРХНОСТИ ЭЛЛИПСОИДА. Связь астрономических долгот и широт с геодезическими. Уклонение отвесной линии. Редуцирование результатов измерений на поверхность эллипсоида. Поверхность относимости. Определение горизонтального проложения. Определение линии между точками на поверхности эллипсоида. ТЕМА 8. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ. Понятие о прямоугольных координатах. Плоские прямоугольные координаты. Оси координат. Ось абсцисс. Ось ординат. Правая система прямоугольных координат. ТЕМА 9. ПОЛЯРНЫЕ СФЕРИЧЕСКИЕ КООРДИНАТЫ. Понятие о полярных координатах. Условная широта. Условная долгота. Зенитное расстояние. Альмукантарат. Вертикал. Системы координат в зависимости от расположения условного полюса. Нормальная система координат. Поперечная система координат. Косая система координат. Вычисление условной широты и зенитного расстояния. Вычисление азимута текущего вертикала. ТЕМА 10. СВЯЗЬ ПЛОСКОЙ ПРЯМОУГОЛЬНОЙ И ПОЛЯРНОЙ СИСТЕМ КООРДИНАТ. Прямая геодезическая задача. Формулировка задачи. Приращения координат. Получение координат точкиB. Обратная геодезическая задача. 6 Формулировка задачи. Вычисление угла положения. Вычисление горизонтального проложения. ТЕМА 11. СБЛИЖЕНИЕ МЕРИДИАНОВ И ЕГО ОПРЕДЕЛЕНИЕ. Углы сближения меридианов. Пример определения величины сближения меридианов для шара радиусомR. ТЕМА 12. ИСПОЛЬЗОВАНИЕ ПРОЕКЦИИ ГАУССА– КРЮГЕРА В ГЕОДЕЗИИ. Проекция Гаусса-Крюгера. Геометрическая интерпретация проекции. Использование проекцииГаусса-Крюгерав геодезии. Зональная система координат. Искажение в проекцииГаусса-Крюгера. Искажения в длинах линий. Искажения углов. ТЕМА 13. ВЫЧИСЛЕНИЕ ДЛИН ДУГ МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ. Вычисление длины дуги меридиана. Рабочая формула для вычисления длины дуги меридиана. Измерение длины дуги параллели. Рабочая формула для вычисления длины дуги параллели в линейной мере. Получение длин дуг меридианов и параллелей в сантиметрах. ТЕМА 14. ОРИЕНТИРОВАНИЕ ЛИНИЙ. Ориентирные углы направлений. Геодезический азимут. Астрономический азимут. Магнитный азимут. Дирекционный угол. Румб. Связь и взаимное преобразование ориентирных углов. Сближение меридианов. Магнитное склонение. Измерение ориентирных углов. 2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ПО ГЕОДЕЗИЧЕСКИМ ОСНОВАМ КАРТ 2.1. Фигура и размеры Земли Изучение фигуры Земли относится к числу древнейших научных проблем естествознания, определенных потребностями практической деятельности человека. Впервые идея о шарообразности Земли была выдвинута, вероятно, халдейскими жрецами вVI в. до н.э. С таким же утверждением выступал грек Филолай(V в. до н. э.). Ту же мысль высказывал Аристотель вIV в. до н. э. В качестве доказательства они ссылались на то обстоятельство, что шар— это самая«совершенная» из геометрических форм. Наблюдения за уходящими за горизонт кораблями также наталкивали на мысль о том, что Земля круглая. И.Ньютон в опубликованном трактате в1687 г. «Математические начала натуральной философии» утверждал, чтоиз-завращения вокруг своей оси Земля должна быть сплюснутой у полюсов и представлять собой сфероид или эллипсоид вращения, т. е. фигуру, которая получается, если вращать эллипс вокруг малой оси. Эта идея требовала подтверждения. Для этого Парижская академия наук организовала две экспедиции: одну в Перу поближе к экватору, другую в Лапландию— на север Финляндии. Экспедиции должны были произвести измерения длин дуг меридианов, один градус которых, если Земля действительно сплюснута у полюсов, должен быть неодинаков на севере и на юге. Для измерения длин дуг меридианов в XVII в.голландский астроном и математик В.Снеллиус предложил метод триангуляции. Поверхность Земли, представляющую сложное сочетание неровностей суши иокеанов, называют физической или топографической поверхностью. В1873 г. физик И. Б. Листинг предложил использовать для описания формы Земли понятие«геоид» (от греч. «ге» — земля и«ей-дос» — вид). Таким образом получилось, что форма Земли«земле-подобна». Несмотря на странность такого термина, он подчеркивает индивидуальность Земли и поэтому, вероятно, распространился среди геодезистов. Под геоидом понимается уровенная поверхность морей и океанов (безприливов-отливов, сгонов и нагонов), продолженная под материками. Во всех точках уровенной поверхности геоида отвесная линия перпендикулярна касательной к данной точке. Очевидно, что форма геоида связана с распределением масс в теле Земли, вращением ее вокруг оси, взаимодействием сил тяжести и центробежных сил. Поэтому фигура геоида оказалась достаточно сложной и, как позднее установили, принципиально неопределимой. В связи с этим выдающийся отечественный ученый М.С. Молоденский предложил перейти к поверхности«квазигеоида» (якобы«геоида»), которая однозначно определяется по наземным измерениям и совпадает с геоидом на морях и океанах и очень близко подходит к нему на суше. Для научного и практического использования выбрана простая математическая аппроксимация фигуры Земли — земной эллипсоид, или эллипсоид вращения, размеры которого подбираются при условии наилучшего соответствия фигуре квазигеоида для Земли в целом или отдельных ее частей. Эллипсоид, подходящий для всей Земли, называют«общеземным эллипсоидом», а для территории отдельной страны или нескольких стран— «референц-эллипсоидом». Основными параметрами эллипсоида являются большая экваториальная полуось (a), малая полярная полуось(b) (Рис.1), полярное сжатие(α), первый эксцентриситет меридионального эллипса(e). Данные величины взаимосвязаны между собой следующим образом: ; ; ; Рис.1. Эллипсоид вращения Вычисление и уточнение размеров земного эллипсоида, начатое еще вXVIII в., продолжается по сей день. Многие исследователи, пользуясь раз- ными исходными данными и методиками расчета, получают неодинаковые результаты. Поэтому исторически сложилось так, что в разные времена и в разных странах были приняты и законодательно закреплены различные эллипсоиды, и их параметры не совпадают между собой. В 1940 г. отечественные ученые Ф. Н. Красовский и А. А. Изотов завершили вычисление размеровреференц-эллипсоидадля геодезических построений и картографирования территории бывшего СССР. В1946 г. он был введен для всеобщего использования. Параметры эллипсоида Красовского таковы: большая полуось(радиус
В США и Канаде до недавнего времени использовали эллипсоид Кларка, рассчитанный еще в1866 г., его большая полуось на39 м короче, чем в российском эллипсоиде, а сжатие определено в1:295,0. Во многих странах Западной Европы и некоторых государствах Азии принят эллипсоид Хейфорда, вычисленный в1909 г., а в бывших английских колониях— в Индии и странах Южной Азии, используют рассчитанный англичанами в1830 г. эллипсоид Эвереста. В1984 г. на основе спутниковых измерений вычислен международный эллипсоидWGS-84 (World Geodetic System). Всего в мире насчитывается около полутора десятков разных эллипсоидов. 2.2. Понятие о геодезических сетях Геодезическая сеть представляет собой совокупность закрепленных на земной поверхности пунктов, положение которых определено в единой системе координат. Положение опорных пунктов на местности может определятся несколькими способами: 1. Астрономический способ. Он заключается в определении геодезических координат каждого пункта путем наблюдения небесных светил. studfiles.net Занимательная геодезия / ХабрВсем привет! Сегодня я расскажу тебе, %USERNAME%, о башмаках и сургуче, капусте, королях координатах, проекциях, геодезических системах и совсем чуть-чуть о веб-картографии. Устраивайся поудобнее.Как говорил ещё Артур Кларк, любая достаточно развитая технология неотличима от магии. Так и в веб-картографии — я думаю, все давно привыкли пользоваться географическими картами, но далеко не каждый представляет себе, как это всё работает. Вот, казалось бы, простая вещь — географические координаты. Широта и долгота, что может быть проще. А вот представьте, что вы очутились на необитаемом острове. Смартфон утонул, а других средств связи у вас нет. Остаётся только написать письмо с просьбой о помощи и по старинке выбросить его в море в запечатанной бутылке. Вот только незадача — вы совершенно не знаете, где находится ваш необитаемый остров, а без указания координат никто вас не найдёт, даже если выловит ваше письмо. Что делать? Как определить координаты без GPS? Итак, немного теории для начала. Чтобы сопоставить точкам на поверхности сферы координаты, необходимо задать начало отсчета — фундаментальную плоскость для отсчёта широт и нулевой меридиан для отсчёта долгот. Для Земли обычно используются плоскость экватора и гринвичский меридиан соответственно. Широтой (обычно обозначается φ) называют угол между направлением на точку из центра сферы и фундаментальной плоскостью. Долготой (обычно обозначается θ или λ) называют угол между плоскостью проходящего через точку меридиана и плоскостью нулевого меридиана. Как же определить свою широту, т.е. угол между плоскостью земного экватора и точкой, в которой ты находишься? Посмотрим на тот же чертёж под другим углом, спроецировав его на плоскость нашего меридиана. Добавим также к чертежу плоскость горизонта (касательную плоскость к нашей точке): Видим, что искомый угол между направлением на точку и плоскостью экватора равен углу между плоскостью горизонта и осью вращения Земли. Итак, как же нам найти этот угол? Вспомним красивые картинки звёздного неба с большой выдержкой: Вот эта точка в центре всех описываемых звездами окружностей — полюс мира. Измерив её высоту над горизонтом, мы получим широту точки наблюдения. Остаётся вопрос, как найти полюс мира на звёздном небе. Если вы в Северном полушарии, то всё довольно просто: — найдите ковш Большой Медведицы; — проведите мысленно прямую через две крайние звезды ковша — Дубхе и Мерак; — эта прямая укажет вам на ручку ковша Малой Медведицы. Крайняя звезда этой ручки — Полярная — почти в точности совпадает с Северным Полюсом мира. Полярная звезда всегда находится на севере, а её высота над горизонтом равна широте точки наблюдения. Если вас угораздит попасть на Северный полюс, Полярная звезда будет у вас точно над головой. В Южном полушарии всё не так просто. Рядом с южным полюсом мира нет крупных звёзд, и вам придётся найти созвездие Южный Крест, мысленно продлить вниз его бОльшую перекладину и отсчитать 4.5 её длины — где-то в этой области будет находиться южный полюс мира. Само созвездие найти легко — вы много раз видели его на флагах разных стран — Австралии, Новой Зеландии и Бразилии, например. С широтой определились. Перейдём к долготе. Как определить долготу на необитаемом острове? На самом деле, это очень непростая проблема, потому что, в отличие от широты, точка отсчета долготы (нулевой меридиан) выбирается произвольным образом и ни к каким наблюдаемым ориентирам не привязана. Испанский король Филипп II в 1567 году назначил солидное вознаграждение тому, кто предложит метод определения долготы; в 1598 году при Филиппе III оно доросло до 6 тысяч дукатов единовременно и 2 тысячи дукатов ренты пожизненно — очень приличная сумма по тем временам. Задача определения долготы в течение нескольких десятилетий была идеей фикс математиков, как теорема Ферма в 20-м веке. В итоге, долготу стали определять с помощью вот этого прибора: По сути, этот прибор остаётся самым надёжным способом определения долготы (не считая GPS/Глонасс) и в наши дни. Этот прибор… (барабанная дробь)… морской хронометр. В самом деле, при изменении долготы меняется часовой пояс. По разнице локального времени и гринвичского легко определить собственную долготу, причём очень точно. Каждая минута разницы времён соответствует 15 угловым минутам долготы. Соответственно, если у вас есть часы, настроенные по гринвичскому времени (на самом деле, неважно по какому — достаточно знать часовой пояс того места, по времени которого идут ваши часы) — не спешите их переводить. Дождитесь местного полдня, и разница времён подскажет вам долготу вашего острова. (Определить момент полдня очень легко — следите за тенями. В первой половине дня тени укорачиваются, во второй — удлиняются. Момент, когда начали удлиняться тени — астрономический полдень в данной местности.) Оба метода определения координат, кстати, хорошо описаны в романе Жюля Верна «Таинственный остров». Итак, мы сумели определить свою широту и долготу с погрешностью в несколько градусов, т.е. пару сотен километров. Для записки в бутылке такой точности, быть может, ещё хватит, а вот для географических карт уже нет. Частично эта погрешность обусловлена несовершенством используемых инструментов, но есть и другие источники ошибок. Землю можно считать шаром только в первом приближении — вообще же Земля совсем не шар, а геоид — тело, больше всего похожее на сильно неровный эллипсоид вращения. Для того, чтобы точно приписать каждой точке земной поверхности координаты нужны правила — каким образом конкретную точку на геоиде спроецировать на сферу. Такой набор правил должен быть универсальным для всех географических карт в мире — иначе одни и те же координаты будут в разных системах обозначать разные точки земной поверхности. В настоящий момент практически все географические сервисы используют единую систему присвоения точке координат — WGS 84 (WGS = World Geodetic System, 84 — год принятия стандарта). WGS 84 определяет т.н. референсный эллипсоид — повехность, к которой приводятся координаты для удобства вычислений. Параметры этого эллипсоида следующие: — большая полуось (экваториальный радиус): a = 6378137 метров; — сжатие: f = 1 / 298.257223563. Из экваториального радиуса и сжатия можно получить полярный радиус, он же малая полуось (b = a * (1 — f) ≈ 6356752 метра). Любой точке земной поверхности, таким образом, ставится в соответствие три координаты: долгота и широта (на референсном эллипсоиде) и высота над его поверхностью. В 2004 году WGS 84 был дополнен стандартом Earth Gravitational Model (EGM96), который уточняет уровень моря, от которого отсчитываются высоты. Интересно, что нулевой меридиан в WGS 84 вовсе не гринвичский (проходящий через ось пассажного инструмента Гринвичской обсерватории), а т.н. IERS Reference Meridian, который проходит на 5.31 угловой секунды восточнее гринвичского. Допустим, мы научились определять свои координаты. Теперь нужно научиться отображать накопленные географические знания экране монитора. Да вот незадача — сферических мониторов в мире как-то не очень много (не говоря уже о мониторах в форме геоида). Нам нужно каким-то образом отобразить карту на плоскость — спроецировать. Один из самых простых способов — спроецировать сферу на цилиндр, а потом развернуть этот цилиндр на плоскость. Такие проекции называются цилиндрическими, их характерное свойство — все меридианы отображаются на карте вертикальными прямыми. Проекций сферы на цилиндр можно придумать много. Наиболее известная из цилиндрических проекций — проекция Меркатора (по имени широко использовавшего её в своих картах фламандского картографа и географа Герарда Кремера, более известного под латинизированной фамилией Меркатор). Математически она выражается следующим образом (для сферы): x = R · λ; y = R · ln(tg(π/4 + φ/2), где R — радиус сферы, λ — долгота в радианах, φ — широта в радианах. На выходе получаем обычные декартовы координаты в метрах. Карта в проекции Меркатора выглядит вот так: Легко заметить, что проекция Меркатора очень существенно искажает формы и площади объектов. Например, Гренландия на карте занимает в два раза большую площадь, чем Австралия — хотя в реальности Австралия в 3.5 раза больше Гренландии. Чем же так хороша эта проекция, что стала так популярна несмотря на существенные искажения? Дело в том, что у проекции Меркатора есть важное характеристическое свойство: она сохраняет углы при проецировании. Допустим, мы хотим проплыть от Канарских островов к Багамским. Проведём прямую линию на карте, соединяющую точки отправления и прибытия. Так как все меридианы в цилиндрических проекциях параллельны, а проекция Меркатора ещё и сохраняет углы, то наша линия пересечёт все меридианы под одинаковым углом. А это означает, что проплыть вдоль этой линии нам будет очень просто: достаточно сохранять на всём протяжении путешествия один и тот же угол между курсом судна и направлением на полярную звезду (или направлением на магнитный север, что менее точно), причём нужный угол можно легко измерить банальным транспортиром. Подобные линии, пересекающие все меридианы и параллели под одинаковым углом, называются локсодромами. Все локсодромы в проекции Меркатора изображаются прямыми на карте, и именно это замечательное свойство, крайне удобное для морской навигации, и принесло меркаторовской проекции широкую популярность среди моряков. Следует заметить, что сказанное не совсем верно: если мы проецируем сферу, а движемся по геоиду, то путевой угол определится не совсем верно и приплывём мы не совсем туда. (Расхождение может быть довольно заметным — всё-таки, экваториальный и полярный радиусы Земли различаются более чем на 20 километров.) Эллипсоид тоже можно спроецировать с сохранением углов, хотя формулы для эллиптической проекции Меркатора значительно сложнее, чем для сферической (обратное преобразование вообще не выражается в элементарных функциях). Полное и подробное описание математики проекции Меркатора на эллипсоиде можно найти здесь. Когда мы в Яндексе начинали делать свои карты, нам показалось логичным использовать эллиптическую меркаторовскую проекцию. К сожалению, многим другим картографическим веб-сервисам так не показалось, и они используют сферическую проекцию. Поэтому долгое время нельзя было показывать поверх карты Яндекса тайлы, скажем, OSM — они расходились по оси y, чем ближе к полюсу — тем заметнее. В версии API 2.0 мы решили не плыть против течения, и предоставили возможность как работать с картой в произвольной проекции, так и показывать на карте одновременно несколько слоёв в разных проекциях — как удобнее. Путешествовать по локсодроме очень просто, но за эту простоту приходится платить: локсодрома отправит вас в путешествие по неоптимальному маршруту. В частности, путь вдоль параллели (если это не экватор) не является кратчайшим! Для того, чтобы найти кратчайший путь на сфере, нужно провести окружность с центром в центре сферы, проходящую через эти две точки (или, что то же самое, пересечь сферу с плоскостью, проходящей через две точки и центр сферы). Невозможно спроецировать сферу на плоскость так, чтобы кратчайшие пути при этом переходили в прямые отрезки; проекция Меркатора, разумеется, не исключение, и ортодромы в ней выглядят сильно искаженными дугами. Некоторые пути (через полюс) в проекции Меркатора корректно изобразить невозможно: Примерно так проецируется кратчайший путь из Анадыря в Кардифф: сначала улетаем в бесконечность строго на север, а потом возвращаемся из бесконечности строго на юг. В случае движения по сфере кратчайшие пути строятся довольно просто с помощью аппарата сферической тригонометрии, а вот в случае эллипсоида задача существенно усложняется — кратчайшие пути не выражаются в элементарных функциях. (Замечу, что эта проблема, конечно же, не решается выбором сферической проекции Меркатора — построение кратчайших путей осуществляется на референсном эллипсоиде WGS 84 и никак не зависит от параметров проекции.) В ходе разработки API Яндекс.Карт версии 2.0 перед нами встала непростая задача — параметризовать построение кратчайших путей так, чтобы: — можно было легко пользоваться встроенными функциями для расчета кратчайших путей на эллипсоиде WGS 84; — можно было легко задать собственную систему координат с собственными методами расчета кратчайших путей. API Карт ведь можно использовать не только для показа карт земной поверхности, но и, скажем, поверхности Луны или какого-нибудь игрового мира. Для построения кратчайших путей (геодезических линий) в общем случае используется следующее простенькое и незатейливое уравнение: Здесь — т.н. символы Кристоффеля, выражающиеся через частные производные фундаментального метрического тензора. Заставлять пользователя ТАКИМ образом параметризовать свою область картографирования нам показалось несколько негуманным :). Поэтому мы решили пойти другим путём, более приближенным к Земле и потребностям наших пользователей. В геодезии проблемы построениях кратчайших путей составляют т.н. первую (прямую) и вторую (обратную) геодезические задачи. Прямая геодезическая задача: дана исходная точка, направление движения (обычно — путевой угол, т.е. угол между направлением на север и направлением движения) и пройденное расстояние. Требуется найти конечную точку и конечное направление движения. Обратная геодезическая задача: даны две точки. Требуется найти расстояние между ними и направление движения. Обратите внимание, что направление движения (путевой угол) — непрерывная функция, которая изменяется на протяжении всего пути. Имея в своём распоряжении функции решения этих задач, мы с их помощью можем решить необходимые нам кейсы в API Карт: вычисление расстояний, отображение кратчайших путей и построение окружностей на земной поверхности. Мы заявили следующий интерфейс для пользовательских координатных систем: solveDirectProblem(startPoint, direction, distance) — Решает так называемую первую (прямую) геодезическую задачу: где мы окажемся, если выйдем из указанной точки в указанном направлении и пройдём, не сворачивая, указанное расстояние. solveInverseProblem(startPoint, endPoint, reverseDirection) — Решает так называемую вторую (обратную) геодезическую задачу: построить кратчайший маршрут между двумя точками на картографируемой поверхности и определелить расстояние и направление движения. getDistance(point1, point2) — возвращает кратчайшее (вдоль геодезической линии) расстояние между двумя заданными точками (в метрах). (Функция getDistance выделена отдельно для тех случаев, когда расчет расстояний можно выполнить намного быстрее, чем решение обратной задачи.) Этот интерфейс показался нам достаточно простым для реализации в случаях, если пользователь картографирует какую-то нестандартную поверхность или пользуется нестандартными координатами. Со своей стороны мы написали две стандартных реализации — для обычной декартовой плоскости и для референсного эллипсоида WGS 84. Для второй реализации мы использовали формулы Винсенти. Кстати, непосредственно реализовывал эту логику runawayed, передаём ему привет :). Все эти геодезические возможности доступны в API Яндекс.Карт, начиная с версии 2.0.13. Welcome! habr.com Решение задач по топографической карте. | Инженерная геодезия. Часть 1.Измерение расстояний на картах и планах. Для измерения расстояния на карте его берут на циркуль-измеритель и переносят на помещённый под южной рамкой карты линейный масштаб.Более точно расстояние измеряют линейкой с миллиметровыми делениями. Отсчёт по линейке, выраженный в сантиметрах, умножают на число метров, указанное в именованном масштабе карты.
Ещё точнее измерения выполняются с применением поперечного масштаба (рис. 4.5.). На металлической линеечке через m интервалов выгравированы параллельные линии – горизонтали (обычно m = 10). К ним восставлены перпендикуляры – вертикали, расстояние между которыми называют основанием масштаба d (обычно d = 2 см). Крайнее левое основание разделено на n частей и через полученные точки проведено n наклонных линий – трансверсалей (обычно n =10 или 5). Длины отрезков, параллельных основанию, на поперечном масштабе равны: между соседними вертикалями – d, между соседними трансверсалями – d/n. Длины отрезков между вертикалью и исходящей из той же точки трансверсалью изменяются в пределах от 0 до d/n. Наименьшее деление поперечного масштаба, определяющее его точность, равно d/(mn). Для удобства пользования поперечным масштабом деления основания и горизонтали оцифровывают в соответствии с масштабом плана. Оцифровка на рисунке соответствует масштабу 1:500. Для измерения расстояния берут его в раствор циркуля-измерителя. Правую его ножку ставят на одну из вертикалей поперечного масштаба, а левую – на одну из трансверсалей, но так, чтобы обе ножки оказались на одной и той же горизонтали. Измеренное расстояние равно сумме расстояний, соответствующих числу охваченных раствором циркуля целых оснований, десятых долей основания и сотых, оцениваемых по положению ножки циркуля на трансверсали. На рисунке отрезок ab имеет длину 20+3+0,7=23,7 м. Длина отрезка cd равна 30+5+0,45=35,45 м. Из второго примера видно, что длину отрезка удаётся измерить с точностью половины наименьшего деления (в данном случае 0,05 м). Для измерения длин извилистых линий служит специальный прибор - курвиметр, снабжённый колёсиком, которое прокатывают вдоль измеряемой линии. Вращение передаётся на стрелку циферблата, по которому прочитывают измеренное расстояние. Определение координат точек. Для определения географических координат служит минутная рамка карты. Через круглые значения минут широты на западной и восточной рамках южнее определяемой точки прочерчивают линию. На рис. 4.6, а показан отрезок такой линии с широтой 57°20¢. Взяв на циркуль-измеритель расстояние а от определяемой точки M до прочерченной линии, откладывают его на рамке карты и, по десятисекундным делениям соображают число секунд. На рисунке широта точки M равна 57°20¢32". Для определения долготы через одинаковые значения минут на северной и южной рамках прочерчивают вертикальную линию. Расстояние от точки до линии переносят измерителем на северную или южную рамку и соображают число секунд. Прямоугольные координаты определяют, пользуясь километровой сеткой, линии которой параллельны координатным осям x и y. Координаты точки P (рис. 4.6, б) определяются по формуле xP= xю+ Dx, yP= yз+ Dy, где xю и yз - значения координат на линиях сетки, проходящих южнее и западнее точки Р. Они подписаны (в километрах) на выходах линий за рамку. Отрезки Dx и Dy измеряют.
Рис. 4.6. Определение координат точек: а - географических; б – прямоугольных. Повысить точность определения координат точки Р можно, измерив расстояния a и b до ближайших южной и северной линий сетки, а также расстояния c и d до ближайших западной и восточной линий сетки. Отрезки Dx и Dy, выраженные в метрах, вычисляют по формулам
где множитель 1000 - длина стороны квадрата километровой сетки в метрах. Дополнительный эффект измерения отрезков a, b, c, d и использования формул (4.1) состоит в ослаблении погрешностей, вызванных деформацией бумаги. Такой же прием может быть применен и при определении географических координат. Определение углов ориентирования. Дирекционный угол направления отрезка на карте измеряют транспортиром как угол, отсчитываемый по направлению часовой стрелки от северного направления линии километровой сетки до направления отрезка. При необходимости перед измерением отрезок удлиняют до пересечения с линией сетки. Для определения азимута А направления сначала измеряют его дирекционный угол a. Затем вычисляют азимут: А=a+g, где g - сближение меридианов, значение которого подписано под южной рамкой карты и показано на помещённой там же схеме. Можно азимут измерить и непосредственно. Через одноименные значения минут долготы проводят вертикальную линию - меридиан. Угол между северным направлением меридиана и направлением отрезка и есть азимут. Под южной рамкой карты и на схеме указано также склонение магнитной стрелки d, позволяющее вычислить магнитный азимут направления по формуле Ам= А-d. Определение высот точек. Высота точки, лежащей на горизонтали, равна высоте горизонтали. Высоты отдельных горизонталей подписаны в их разрыве. Высоты других горизонталей легко сообразить, зная высоту сечения рельефа, а также высоты подписанных горизонталей и высоты тех характерных точек рельефа, у которых подписаны их отметки. При этом учитывают, что высоты горизонталей кратны высоте сечения рельефа. Высота точки M, расположенной между двумя горизонталями (рис. 4.7) определяется по формуле
где Hг - высота меньшей горизонтали, h – высота сечения рельефа, а отрезки a и b – заложение ската и расстояние от точки до горизонтали, измеряемые по карте линеечкой. Построение профиля. Для построения профиля по линии, проведенной на карте, определяют высоты точек в местах её пересечения с горизонталями, водораздельными и водосливными линиями. Измеряют горизонтальные расстояния до них от начальной точки линии. При построении профиля по горизонтальной оси откладывают расстояния, а по вертикальной - высоты. Для наглядности вертикальный масштаб принимают крупнее горизонтального (в 10, а то и в 50 раз). Определение уклонов и углов наклона. Отрезки линий на земной поверхности обычно имеют наклон, отчего начало и конец отрезка находятся на разных высотах. Разность их высот – превышение, а проекция отрезка на горизонтальную плоскость – его горизонтальное проложение. Уклоном i линии называется отношение превышения h к горизонтальному проложению d: i = h / d. (4.2) Для определения по карте уклона линии на участке KL между двумя горизонталями (рис. 4.7) измеряют его горизонтальное проложение – заложение d. Поскольку концы отрезка лежат на смежных горизонталях, превышение h между ними равно высоте сечения рельефа, подписанному под южной рамкой карты. Воспользовавшись формулой (4.2), вычисляют уклон, который принято выражать в тысячных. Если, например, h=1 м, d=48 м , то уклон равен i =1 м / 48 м = 0,021=21‰.
С другой стороны, отношение превышения h к горизонтальному проложению d равно тангенсу угла n наклона линии. Поэтому i = tg n, что позволяет, вычислив уклон определить по нему угол наклона. При пользовании картой углы наклона не вычисляют, а определяют с помощью графика заложений (рис. 4.8), расположенного под южной рамкой карты. По горизонтальной оси графика отложены углы наклона, а по вертикальной - соответствующие этим углам заложения d, выраженные в масштабе карты и рассчитанные по формуле d = h ¤ (M tg n), где h - высота сечения рельефа, а M – знаменатель масштаба карты.
Для определения угла наклона отрезка KL (рис. 4.7), расположенного между горизонталями, берут его в раствор циркуля и на графике заложений (рис. 4.8) находят такой угол, над которым ордината равна раствору циркуля d. Это и есть искомый угол наклона. При необходимости многократного определения уклонов пользуются графиком уклонов, построенным аналогично графику заложений, но с отложением по горизонтальной оси не углов наклона, а уклонов. Проведение линии с уклоном, не превышающим заданного предельного. Необходимость решения такой задачи возникает, например, при выборе трассы для будущей дороги. Вычисляют соответствующее заданному предельному уклону iпр заложение, выраженное в масштабе карты,
Чтобы уклон линии не превосходилiпр, ни одно заложение на ней не должно быть меньше, чем рассчитанноеd. Если расстояние между горизонталями больше рассчитанного, направление линии можно выбирать произвольно. В противном случае в раствор циркуля берут отрезок, равный d, и строят ломаную линию, умещая между горизонталями рассчитанное предельное заложение (рис. 4.9). Определение границ водосборной площади (бассейна). Водосборной называют площадь, с которой дождевые и талые воды поступают в данное русло. Определение водосборной площади необходимо, например, при проектировании дороги для расчёта отверстия моста или трубы. Для определения границ водосборной площади на карте проводят водораздельные линии, а затем от проектируемого сооружения к водораздельным линиям проводят линии наибольшего ската, перпендикулярные горизонталям. Например, водосборная площадь, для точки Р, где предстоит строительство трубы, (рис. 4.10), ограничена штриховой линией, образованной водораздельной и двумя линиями наибольшего ската. injzashita.com Геодезия: весь мир на карте! - Статьи
Когда великие путешественники стали открывать на нашей планете всё новые земли, оказалось, что Земля на самом деле просто огромна и абсолютно не представляется возможным удержать все сведения о ней в уме. В те времена также требовалось наносить на карты караванные пути, горные тропинки и перевалы, реки и броды, колодцы в пустыне и места укрытия для путников. Точные измерения земной поверхности, а также перенесение этих данных на карты и планы в масштабе - это и есть основная задача геодезии - одной из самых древних наук на Земле. Геодезия в буквальном смысле слова «разделяет землю» на части и определяет с высокой степенью точности её размеры и форму. В геодезии измерения производятся при помощи самых различных геодезических приборов, которые помогают определять расстояния до различных видимых объектов, а также от одного ориентира до другого. На сегодняшний день в арсенале геодезистов имеются даже лазерные измерительные приборы и приборы спутниковой навигации. Для определения положения практически любой точки земной поверхности применяют три координаты: долготу и широту, которые указывают положение объекта на земной поверхности, а также высоту над нулевым уровнем - уровнем моря, что определяет действительное положение объекта в трехмерном пространстве. В очень точном определении этих трех параметров, можно сказать, и состоит основная задача геодезии земли. Все основные геодезические методы съемки как раз и направлены на решение этого вопроса. Выполнение геодезических изысканий для нового строительства обеспечивает наработку необходимых материалов геодезии земельного участка для данного объекта. При этом уточняется рельеф местности, а также положение уже существующих зданий и элементов планировки. Геодезические изыскания выполняются в определенной последовательности. В их состав входит геодезическая съемка местности, подземных и надземных сооружений, а также инженерных коммуникаций. Также геодезические изыскания могут в себя включать Любой проект предусматривает получение необходимых геодезических данных, определение и привязку к местности основных осей и границ зданий в соответствии с проектом, а также соблюдение в процессе строительства геометрических форм и размеров готового здания и всех его конструкций. Геодезическая съемка земельного участка производится с целью формирования границ нового земельного участка или уточнения границ старого. Также геодезию земельного участка производят и для подготовки межевого плана. Вообще, геодезическая съемка - это достаточно широкий комплекс геодезических работ. Её начальный этап проводится на местности, а основная расчетная и графическая работа производится уже в так называемых камеральных условиях (то есть, говоря простым языком – в помещении). В результате проведения геодезических работ получается достаточно подробный план земельного участка со всеми существующими строениями, выделением границ и привязкой к границам соседних участков и различным техническим коммуникациям. Такой подробный план земельного участка носит название геоподосновы. Вообще, геодезия в строительстве - это целый комплекс измерений, вычислений и построений в чертежах и натуре, обеспечивающих правильное размещение зданий и сооружений, а также правильное возведение их конструктивных элементов. При строительстве достаточно крупных и сложных инженерных объектов для выполнения геодезических работ на строительной площадке не редко привлекаются специализированны Организация геодезических работ в строительстве представляет собой комплекс очень ответственных мероприятий, от которых напрямую зависит успех всего строительного процесса. Ну, а качество этих работ существенно зависит от профессионализма специалистов, выполняющих работы, а также от точности используемых при этом приборов и оборудования.  Зарегистрируйтесь, чтобы голосовать! Проголосовало: 0 Оценка: 0 poremontu.ru Геодезическая основа картГеодезическая основа картСведения о геодезической основе картВ геодезии под общим видом Земли понимают некоторую воображаемую уровенную поверхность, совпадающую с поверхностью воды в океанах и морях в спокойном ее состоянии, мысленно продолженную под материками, при условии перпендикулярности ее во всех своих точках к отвесным линиям, т. е. к линиям направления силы тяжести. Эта уровенная поверхность называется пове6рхностью геоида, а геометрическое тело, ограниченное ею, называется геоидом. Ввиду неравномерного по плотности распределения масс в земной коре направление отвесной линии испытывает при перемещении по земной поверхности различные отклонения от направления нормали к эллипсоиду, благодаря чему поверхность геоида имеет многочисленные отступления от поверхности эллипсоида. Следовательно, поверхность геоида представляет собой неправильную, нематематическую форму, которая нам неизвестна и не может быть применена для проектирования на нее физической поверхности Земли. Отсюда вытекает необходимость замены поверхности геоида другой поверхностью, более простой и возможно ближе подходящей к поверхности геоида. Из наиболее простых математических поверхностей к поверхности геоида ближе всего подходит поверхность эллипсоида вращения с малым сжатием у полюсов. Эллипсоидом вращения называется тело, полученное от вращения эллипса вокруг одной из его осей. Эллипсоид вращения с малым сжатием за его близость к шару иногда называют сфероидом. Обычно же для краткости его именуют просто эллипсоидом. Общим земным эллипсоидом называется такой эллипсоид, поверхность которого наиболее близка к поверхности геоида в целом. В настоящее время еще нет условий для определения размеров общего земного эллипсоида. Эти условия наступят, когда градусные измерения в совокупности с гравиметрическими определениями* равномерно покроют всю поверхность земного шара. Размеры местных (частных) земных эллипсоидов, близких к поверхности геоида только в отдельных его частях, вначале на основе только градусных измерений, а затем с учетом гравиметрических определений выводились в разное время многими учеными. Каждому эллипсоиду присвоено имя ученого, определившего его размеры. Наиболее известными являются эллипсоиды Деламбра (1800 год), Вальбека (1819 год), Эйри (1830 год), Бесселя (1841 год), Теннера f (1844 год), Кчарка (1866 и 1880 годы), Хейфорда (1910 год), Хейсканена (1929 год), Красовского (1940 год). Расхождения в определениях размеров полуосей земного эллипсоида по этим выводам не превышают нескольких сот метров. Точность определений размеров земного эллипсоида зависит от объема и точности использованных при выводах градусных измерений и гравиметрических определений. Наибольшее количество высокоточных градусных измерений и гравиметрических определений было использовано при выводе размеров эллипсоида Красовского. Вывод размеров этого эллипсоида производился Центральным научно-исследовательским институтом геодезии, аэрофотосъемки и картографии (ЦНИИГАиК) под руководством проф. Ф. Н. Красовского и А. А. Изотова. Размеры эллипсоида Красовского следующие: Большая полуось а = 6378245 м; Малая полуось b =. 6 356 863 м; Сжатие При вычислении размеров эллипсоида Красовского были использованы не только значительные по объему астрономо-геодезические и гравиметрические измерения, произведенные на территории СНГ, но и материалы астрономо-геодезических и гравиметрических измерений, выполненных в Западной Европе и США. Гравиметрические определения дают возможность измерить силу тяжести в любой точке поверхности Земли как на суше, так и на море. Из гравиметрических определений можно весьма надежно получить сжатие земного эллипсоида. Большой объем материалов, часть из которых впервые была использована для вывода размеров земного эллипсоида, и высокая точность полученных результатов дают достаточное основание считать эллипсоид Красовского наиболее близким к поверхности геоида. Референц-эллипсоид. Исходные геодезические даты. Система геодезических координатРеференц-эллипсоидом называется земной эллипсоид определенных размеров и определенным образом ориентированный в теле Земли, на поверхность которого переносятся результаты всех геодезических и топографических работ. Выбор размеров и ориентирование этого эллипсоида должны удовлетворять требованию наибольшей близости его поверхности к поверхности геоида в пределах территории данного государства. Ориентирование эллипсоида в теле Земли (геоида) означает установление определенных значений географических координат исходного пункта и азимута с него на смежный пункт, а также принятие высоты поверхности эллипсоида над поверхностью геоида в этом пункте. Тот пункт триангуляции, который является исходным и координаты которого определяются астрономическим путем, называется началом триангуляции, а его широта, долгота и азимут с него на смежный пункт называются исходными геодезическими датами (данными). От исходного пункта ведется вычисление геодезических координат всех пунктов триангуляции и полигонометрии на поверхности принятого референц-эллипсоида. Размеры принятого референц-эллипсоида и исходные геодезические даты характеризуют собой систему геодезических координат, в которой вычисляются координаты всех пунктов триангуляции и полигонометрии, используемых в качестве опорных при. топографических, картографических и других работах, связанных с измерениями на земной поверхности. На Украие кабинетом министров Украины постановленим №844 от 8 июня 1998 г. утверждены основные положения создания Государственной геодезической сети Украины. Прежние и современная системы координат на территории СНГ Рассмотрим вкратце системы координат, существовавшие на Украине до 1946 года. Триангуляция 1 класса, проложенная Корпусом военных топографов в прошлом столетии на территории западного пограничного пространства, вычислялась на разных эллипсоидах и от различных исходных геодезических дат. Для объединения всех триангуляции в 1897 году была введена Юрьевская система координат. С 1910 года все новые триангуляции в Европейской России вычислялись в двух системах: к востоку от Пулковского меридиана — в Пулковской системе 1910 года и к западу от него — в Юрьевской системе координат. В 1932 году после получения более точных значений координат Пулковской обсерватории была принята Пулковская система координат 1932 года для всех сетей триангуляции, расположенных к западу от меридиана 96° в. д. К востоку от меридиана 96° в. д. в 1935 году была введена Свободненская система координат с исходным пунктом Черниговский, близ города Свободный. Она заменила собой существовавшие до этого Маньчжурскую и Хабаровскую системы координат. Ее введение было вызвано все увеличивавшимися по мере удаления на восток расхождениями между координатами, вычисленными в Пулковской системе, и астрономическими координатами одних и тех же пунктов. Так, например, в районе города Омск эти расхождения доходили до 10” (300 м). Кроме Свободненской системы, на Дальнем Востоке применялись и другие системы координат. Например, в бассейне реки Колыма координаты пунктов вычислялись с 1932 года в Дебинской системе с исходным пунктом Дебинский. На полуострове Камчатка была принята Петропавловская система координат с исходным пунктом Николаевка, близ города Петропавловск-Камчатский. Среднеазиатские триангуляции с 1875 года вычислялись в Ташкентской системе координат. Вычисление триангуляции во всех системах производилось на эллипсоиде Бесселя. Счет долгот велся от Гринвичского меридиана, за исключением Пулковской (1910 года) и Юрьевской (1897 года) систем, в которых долготы исчислялись от Пулковского меридиана (к востоку — со знаком плюс, к западу — со знаком минус). Высоты исчислялись от уровня ближайшего моря, принимаемого за нулевой, что приводило к расхождению в высотах одного и того же пункта, определенных в разных системах. Геодезическая связь между триангуляциями, вычисленными в двух основных системах координат—Пулковской и Свободненской— была установлена незадолго до Великой Отечественной войны 1941—1945 годов. В результате сопоставления координат общих пунктов триангуляции оказалось, что вблизи меридиана 96° в. д. координаты одних и тех же пунктов, вычисленные в разных системах, различались между собой в линейном выражении до 900 м. Значительно расходились они и с астрономическими координатами этих же пунктов. Все это свидетельствовало о том, что эллипсоид Бесселя по своим размерам и принятой ориентировке плохо подходил для территории Украины, России, хотя здесь сказались и ошибки в исходных геодезических датах обеих систем. Наличие многосистемности в общегосударственной сети служило причиной:
Приведение триангуляции СНГ к единой системе координат и их переуравнивание требовало своего неотложного решения. Новая, единая для всей территории СНГ Система координат 1942 года, как указывалось, была принята в 1946 году. На издаваемых картах масштабов 1 : 200 000 и крупнее на полях листов помещается надпись: Система координат 1942 года, означающая, что данный лист карты составлен в новой системе. Замена эллипсоида Бесселя эллипсоидом Красовского и переход от различных систем координат к единой Системе координат 1942 года потребовали решения целого ряда сложных задач в области геодезии и картографии. Прежде всего была переуравнена вся триангуляционная сеть 1 класса и получены новые геодезические координаты пунктов, которые были затем перевычислены в плоские прямоугольные координаты в проекции Гаусса. После этого было произведено полное перевычисление плоских прямоугольных координат всех пунктов заполняющих сетей низших классов. Однако переход к Системе координат 1942 года не ограничивается перевычислением координат геодезических пунктов, но вызывает также большие работы в картографическом производстве, связанные с необходимостью перемещения координатных сеток и рамок листов всех ранее изданных топографических карт. Переход от одной системы координат к другой Всякий лист любой топографической карты имеет геодезические пункты, координатную сетку и рамку, которые взаимно связаны между собой той или иной системой координат. Рассмотрим те изменения, которые претерпевают координаты геодезических пунктов, размеры сторон трапеции, координатная сетка и прямоугольные координаты вершин углов рамки трапеции при переходе от одной системы координат к другой. Координаты геодезических пунктов взаимно связаны между собой системой координат и поэтому с изменением последней будут изменяться. Положение геодезических пунктов может быть задано или в геодезических координатах, или в плоских прямоугольных координатах в той или иной проекции (например, в проекции Гаусса, которые обычно называются просто прямоугольными координатами. Изменение геодезических координат пунктов триангуляции может быть следствием трех причин:
Геодезическая основа карт - 4.5 out of 5 based on 2 votes kadastrua.ru
| |||||







![inj_geo_1-26.jpg [image]](/800/600/http/injzashita.com/images/inj_geo_all/inj_geo_1-26.jpg)
![inj_geo_1-27.jpg [image]](/800/600/http/injzashita.com/images/inj_geo_all/inj_geo_1-27.jpg)
![inj_geo_1-28.jpg [image]](/800/600/http/injzashita.com/images/inj_geo_all/inj_geo_1-28.jpg) ,
, ![inj_geo_1-29.jpg [image]](/800/600/http/injzashita.com/images/inj_geo_all/inj_geo_1-29.jpg) , (4.1)
, (4.1)
![inj_geo_1-30.jpg [image]](/800/600/http/injzashita.com/images/inj_geo_all/inj_geo_1-30.jpg) ,
,
![inj_geo_1-31.jpg [image]](/800/600/http/injzashita.com/images/inj_geo_all/inj_geo_1-31.jpg)
![inj_geo_1-32.jpg [image]](/800/600/http/injzashita.com/images/inj_geo_all/inj_geo_1-32.jpg)
![inj_geo_1-33.jpg [image]](/800/600/http/injzashita.com/images/inj_geo_all/inj_geo_1-33.jpg) (здесь M – знаменатель масштаба). .
(здесь M – знаменатель масштаба). .
![inj_geo_1-34.jpg [image]](/800/600/http/injzashita.com/images/inj_geo_all/inj_geo_1-34.jpg)
![inj_geo_1-35.jpg [image]](/800/600/http/injzashita.com/images/inj_geo_all/inj_geo_1-35.jpg)

 На самом деле это непростая задача, ведь кривизна поверхности нашей планеты различна на каждой широте и долготе. Именно потому земную поверхность не так-то и просто отобразить на карте, особенно, если эта карта крупномасштабная. Для этих целей проводится множество точных измерений, и рисуются целые тома различных подробных карт в малом масштабе, на которых отображаются даже отдельные деревья и крупные камни. И не перестают шагать по миру группы геодезистов со своими теодолитами, проверяя и перепроверяя уже измеренные просторы, а также внося новые штрихи в отображение на бумаге современной картины мира.
На самом деле это непростая задача, ведь кривизна поверхности нашей планеты различна на каждой широте и долготе. Именно потому земную поверхность не так-то и просто отобразить на карте, особенно, если эта карта крупномасштабная. Для этих целей проводится множество точных измерений, и рисуются целые тома различных подробных карт в малом масштабе, на которых отображаются даже отдельные деревья и крупные камни. И не перестают шагать по миру группы геодезистов со своими теодолитами, проверяя и перепроверяя уже измеренные просторы, а также внося новые штрихи в отображение на бумаге современной картины мира. наблюдения за деформациями зданий, земной поверхности и горных пород.
наблюдения за деформациями зданий, земной поверхности и горных пород. е геодезические организации. Обладая современной техникой и имея штат высококвалифицированных сотрудников такие организации достаточно грамотно и быстро способны выполнить весь спектр геодезических работ на всех этапах строительства. Так, проведя предварительный сбор, анализ и обобщение всех материалов по предстоящему строительству специалисты произведут выбор площадки под строительство и проведут все необходимые инженерно-геодезические изыскания. На подготовительном этапе строительства они проведут геодезическую разбивку, а в основной период проконтролируют геометрическое соответствие возводимых подземных и надземных частей зданий и сооружений проекту, а также выполнят исполнительную съемку законченных строительством элементов и подготовят комплект исполнительной геодезической документации к сдаче. Когда же строительство будет полностью завершено, они составят исполнительную топографическую съемку завершенного строительством объекта и внешних инженерных коммуникаций.
е геодезические организации. Обладая современной техникой и имея штат высококвалифицированных сотрудников такие организации достаточно грамотно и быстро способны выполнить весь спектр геодезических работ на всех этапах строительства. Так, проведя предварительный сбор, анализ и обобщение всех материалов по предстоящему строительству специалисты произведут выбор площадки под строительство и проведут все необходимые инженерно-геодезические изыскания. На подготовительном этапе строительства они проведут геодезическую разбивку, а в основной период проконтролируют геометрическое соответствие возводимых подземных и надземных частей зданий и сооружений проекту, а также выполнят исполнительную съемку законченных строительством элементов и подготовят комплект исполнительной геодезической документации к сдаче. Когда же строительство будет полностью завершено, они составят исполнительную топографическую съемку завершенного строительством объекта и внешних инженерных коммуникаций.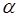 = 1:298,3.
= 1:298,3.







